【题目】四边形
的对角线相交于点
，且
，那么下列条件不能判断四边形为平行四边形的是（ ）
A. 
B. 
C. 
D. 
轻松课堂单元测试AB卷系列答案
小题狂做系列答案科目：初中数学 来源： 题型：
【题目】已知，在
中，
，
，
为直线
上一动点（不与点
，
重合），以
为边作正方形
，连接
.
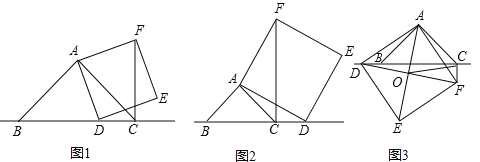
（1）如图1，当点在线段上时，请直接写出：，
，三条线段之间的数量关系为________.
（2）如图2，当点在线段的延长线上时，其他条件不变.（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请你写出正确的结论，并给出证明.
（3）如图3，当点在线段的反向延长线上时，且点
，
分别在直线的两侧，其他条件不变.请直接写出：，，三条线段之间的数量关系______________.
查看答案和解析>>
科目：初中数学 来源： 题型：
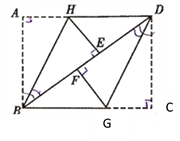
【题目】把一张矩形纸片ABCD按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG.
（1）求证：△BHE≌△DGF；
（2）若AB＝6cm，BC＝8cm，求线段FG的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为6,则重叠部分四边形EMCN的面积为( )
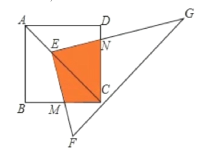
A. 9B. 12C. 16D. 32
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）（49）（＋91）（5）＋（9）;
（2）
（3）3x2-[7x-（4x-3）-2x2]
（4）解方程：x+13=5x+37
（5）先化简，再求值：
，其中x＝﹣3，y＝
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式．下列三个代数式：①（a﹣b）2；②ab+bc+ca；③a2b+b2c+c2a．其中是完全对称式的是（ ）
A. ①②③ B. ①③ C. ②③ D. ①②
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列图形都是由同样大小的基本图形按一定规律所组成的，其中第①个图形中共有5个基本图形，第②个图形中共有8个基本图形，第③个图形中共有11个基本图形，第④个图形中共有14个基本图形，……，按此规律排列，第⑧个图形中共有( )个基本图形
A.23B.24C.26D.29
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某班“数学兴趣小组”对函数
的图象和性质进行了探究，过程如下，请补充完整.
（1）自变量
的取值范围是全体实数，与
的几组对应值列表如下：
| … |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | … |
其中，
__________.
（2）根据上表的数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.
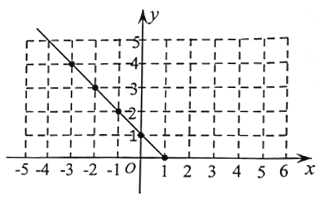
（3）观察图象，写出该函数的两条性质：
①____________________________________________________________
②____________________________________________________________
（4）进一步探究函数图象发现：
①方程
的解是__________.
②方程
的解是__________.
③关于的方程
有两个不相等实数根，则
的取值范围是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为进一步推广“阳光体育”大课间活动，高新中学对已开设的A实心球，B立定跳远，C跑步，D排球四种活动项目的学生喜欢情况进行调查，随机抽取了部分学生，并将调查结果绘制成图1，图2的统计图，请结合图中的信息解答下列问题：
（1）请计算本次调查中喜欢“跑步”的学生人数和所占百分比，并将两个统计图补充完整；
（2）随机抽取了3名喜欢“跑步”的学生，其中有2名男生，1名女生，现从这3名学生中任意抽取2名学生，请用画树状图或列表的方法，求出刚好抽到一男生一女生的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
