
����Ŀ����֪����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣨�����
��һ���㣨�����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ����������
����������![]() ������
������![]() .
.
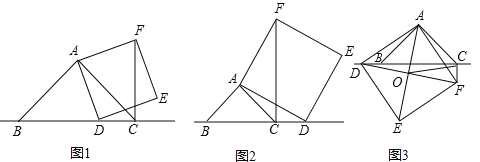
��1����ͼ1������![]() ���߶�
���߶�![]() ��ʱ����ֱ��д����
��ʱ����ֱ��д����![]() ��
��![]() ��
��![]() �����߶�֮���������ϵΪ________.
�����߶�֮���������ϵΪ________.
��2����ͼ2������![]() ���߶�
���߶�![]() ���ӳ�����ʱ��������������.��1���еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�Ľ��ۣ�������֤��.
���ӳ�����ʱ��������������.��1���еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�Ľ��ۣ�������֤��.
��3����ͼ3������![]() ���߶�
���߶�![]() �ķ����ӳ�����ʱ���ҵ�
�ķ����ӳ�����ʱ���ҵ�![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() �����࣬������������.��ֱ��д����
�����࣬������������.��ֱ��д����![]() ��
��![]() ��
��![]() �����߶�֮���������ϵ______________.
�����߶�֮���������ϵ______________.
���𰸡���1��![]() ����2������������ȷ�Ľ��ۣ�
����2������������ȷ�Ľ��ۣ�![]() ������������3��
������������3��![]() .
.
��������
��1��������ABC�ǵ���ֱ�������Σ�����SAS����֤����BAD�ա�CAF���Ӷ�֤��CF=BD���ݴ˼���֤�ã�
��2��ͬ��1����ͬ������SAS����֤�á�BAD�ա�CAF���Ӷ�֤��BD=CF�����ɵõ�CF-CD=BC��
��3������֤����BAD�ա�CAF����FCD��ֱ�������Σ�Ȼ���������������ã�
�⣺��1���ߡ�BAC=90�㣬��ABC=45�㣬
���ACB=��ABC=45�㣬
��AB=AC��
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAD=90��-��DAC����CAF=90��-��DAC��
���BAD=��CAF��
���ڡ�BAD�͡�CAF�У�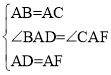 ��
��
���BAD�ա�CAF��SAS����
��BD=CF��
��BD+CD=BC��
��CF+CD=BC��
��2��������
![]() ���������£���ͼ2
���������£���ͼ2
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() .
.
���ı���![]() Ϊ�����Σ�
������
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.
��3�����ݢ٢ڿ�֪��BAD�ա�CAF��SAS����
��BD=CF��DC=BD+BC��
��BC=CD��CF.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��AD��CB��CD��E��CD��һ�㣬BE��AC�ڵ�F������DF.
(1)��֤����BAC����DAC����AFD����CFE��
(2)��AB��CD����֤���ı���ABCD�����Σ�
(3)��(2)�������£���ȷ��E���λ�ã�ʹ��EFD����BCD����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
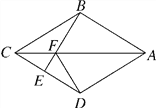
����Ŀ����1����ͼ1����AOC��������BOC��������OMƽ�֡�AOC��ONƽ�֡�BOC�����MON���� �����ú���������ʽ�ӱ�ʾ����
��2����ͼ2��������BOC�Ƶ�O��ʱ����ת30����õ���EOD��OMƽ�֡�AOD��ONƽ�֡�COE�����MON�Ķ������ú���������ʽ�ӱ�ʾ����
��3������BOC��ת90����ͼ3��λ�ã������������䣬���MON�Ķ������� �����ú���������ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϣ���OΪԭ�㣬��A��Ӧ����Ϊ9����B��Ӧ����Ϊb����C�ڵ�B�Ҳ࣬����Ϊ2����λ���߶�BC���������ƶ���
![]()
��1����ͼ�����߶�BC��O��A����֮���ƶ���ijһλ��ʱ��ǡ�������߶�AC��OB�����ʱb��ֵ��
��2�����߶�BC��������������AO�����ƶ��Ĺ����У�������AC��OB��![]() AB�����ʱ����������b��ֵ��
AB�����ʱ����������b��ֵ��
��3�����߶�BC���������ƶ�ʱ�������ϵʽ|AC��OB|��![]() |AB��OC|�����ʱb��ȡֵ��Χ���� ��
|AB��OC|�����ʱb��ȡֵ��Χ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=��![]() x2+bx+c��ͼ��A��2��0����B��0����6��������
x2+bx+c��ͼ��A��2��0����B��0����6��������
��1����������κ����Ľ���ʽ��
��2����ö��κ����ĶԳ�����x�ύ�ڵ�C������BA��BC�����ABC�������
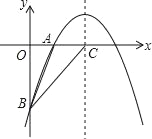
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������繤������,�����������֮���������������Ļ�����������������������������ʽ�ں�Ȼ�㳡���С�Ϊ��ӭ�Ӵ˴�ʢ��,ij����Ʒ���������֯![]() �����˸���һ�������Ʒ��Ϊ�˽�ÿ�����˵��վ���������,���������ij��ÿ�����˵���������������������±�:
�����˸���һ�������Ʒ��Ϊ�˽�ÿ�����˵��վ���������,���������ij��ÿ�����˵���������������������±�:

����һ��![]() ������������������������λ���ֱ��ǣ� ��
������������������������λ���ֱ��ǣ� ��
A. ![]() ����
����![]() ��B.
��B. ![]() ����
����![]() ��C.
��C. ![]() ����
����![]() ��D.
��D. ![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊ
Ϊ![]() ����һ�㣬
����һ�㣬![]() ����
����![]() ��
��![]() ���������ÿ��
���������ÿ��![]() ����λ���ٶ�����
����λ���ٶ�����![]() �����յ�
�����յ�![]() �˶�������
�˶�������![]() �����
�����![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() �룬��
�룬��![]() ��ֵΪ__________ʱ��
��ֵΪ__________ʱ��![]() ����
����![]() Ϊ���ĵ��������Σ�
Ϊ���ĵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������£�ij���˾��ÿ��ݳ���ʻ![]() Сʱ����ƽ���ٶ�Ϊ
Сʱ����ƽ���ٶ�Ϊ![]() ǧ��ʱ����֪����A�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ������B�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ��
ǧ��ʱ����֪����A�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ������B�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ��
��1����A�ճ��˾���������������ʻ����ǧ�ף����ú�![]() ��
��![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����֪A�ճ��˾���������������ʻ120ǧ�ף���B�ճ��˾���������������ʻ����ǧ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() �ĶԽ����ཻ�ڵ�
�ĶԽ����ཻ�ڵ�![]() ����
����![]() ����ô�������������ж��ı���
����ô�������������ж��ı���![]() Ϊƽ���ı��ε��ǣ� ��
Ϊƽ���ı��ε��ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com