
【题目】已知矩形![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,点
,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位的速度沿着
个单位的速度沿着![]() 边向终点
边向终点![]() 运动,连接
运动,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒,则当
秒,则当![]() 的值为__________时,
的值为__________时,![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.
【答案】![]() 或
或![]()
【解析】
根据矩形的性质求出∠D=90°,AB=CD=8,求出DE后根据勾股定理求出AE;过E作EM⊥AB于M,过P作PQ⊥CD于Q,求出AM=DE=3,当EP=EA时,AP=2DE=6,即可求出t;当AP=AE=5时,求出BP=3,即可求出t;当PE=PA时,则x2=(x-3)2+42,求出x,即可求出t.
∵四边形ABCD是长方形,
∴∠D=90°,AB=CD=8,
∵CE=5,
∴DE=3,
在Rt△ADE中,∠D=90°,AD=4,DE=3,由勾股定理得:AE=5
过E作EM⊥AB于M,过P作PQ⊥CD于Q,
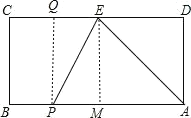
则AM=DE=3,
若△PAE是等腰三角形,则有三种可能:
当EP=EA时,AP=2DE=6,
所以t=![]() =2;
=2;
当AP=AE=5时,BP=85=3,
所以t=3÷1=3;
当PE=PA时,设PA=PE=x,BP=8x,则EQ=5(8x)=x3,
则![]()
解得:x=![]() ,
,
则t=(8![]() )÷1=
)÷1=![]() ,
,
综上所述t=2或![]() 时,△PAE为等腰三角形。
时,△PAE为等腰三角形。
故答案为:2或![]() .
.


科目:初中数学 来源: 题型:
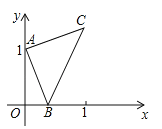
【题目】(2016青海省西宁市)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.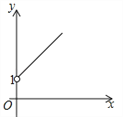 B.
B.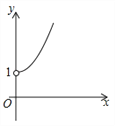 C.
C.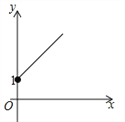 D.
D.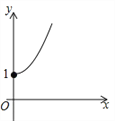
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),以
重合),以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() .
.
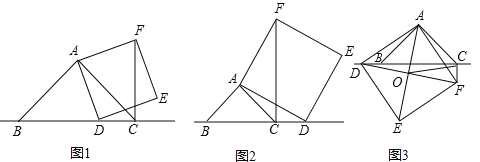
(1)如图1,当点![]() 在线段
在线段![]() 上时,请直接写出:
上时,请直接写出:![]() ,
,![]() ,
,![]() 三条线段之间的数量关系为________.
三条线段之间的数量关系为________.
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,其他条件不变.(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请你写出正确的结论,并给出证明.
的延长线上时,其他条件不变.(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请你写出正确的结论,并给出证明.
(3)如图3,当点![]() 在线段
在线段![]() 的反向延长线上时,且点
的反向延长线上时,且点![]() ,
,![]() 分别在直线
分别在直线![]() 的两侧,其他条件不变.请直接写出:
的两侧,其他条件不变.请直接写出:![]() ,
,![]() ,
,![]() 三条线段之间的数量关系______________.
三条线段之间的数量关系______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠ 1+∠ 2=180°.
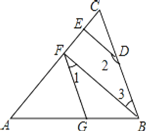
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠CDE=30°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )

A. △CDF≌△EBC
B. ∠CDF=∠EAF
C. CG⊥AE
D. △ECF是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 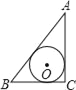 B.
B. 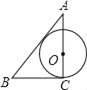 C.
C. 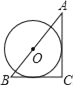 D.
D. 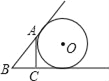
查看答案和解析>>
科目:初中数学 来源: 题型:
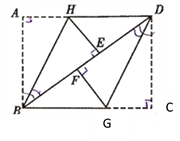
【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的基本图形按一定规律所组成的,其中第①个图形中共有5个基本图形,第②个图形中共有8个基本图形,第③个图形中共有11个基本图形,第④个图形中共有14个基本图形,……,按此规律排列,第⑧个图形中共有( )个基本图形

A.23B.24C.26D.29
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com