
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 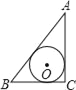 B.
B. 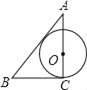 C.
C. 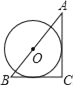 D.
D. 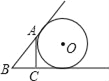
【答案】C
【解析】解:设⊙O的半径为r.
A.∵⊙O是△ABC内切圆,∴S△ABC=![]() (a+b+c)r=
(a+b+c)r=![]() ab,∴r=
ab,∴r=![]() ;
;
B.如图,连接OD,则OD=OC=r,OA=b﹣r.∵AD是⊙O的切线,∴OD⊥AB,即∠AOD=∠C=90°,∴△ADO∽△ACB,∴OA:AB=OD:BC,即(b﹣r):c=r:a,解得:r=![]() ;
;
C.连接OE,OD.∵AC与BC是⊙O的切线,∴OE⊥BC,OD⊥AC,∴∠OEB=∠ODC=∠C=90°,∴四边形ODCE是矩形.∵OD=OE,∴矩形ODCE是正方形,∴EC=OD=r,OE∥AC,∴OE:AC=BE:BC,∴r:b=(a﹣r):a,∴r=![]() ;
;
D.设AC、BA、BC与⊙O的切点分别为D、F、E,连接OD、OE.
∵AC、BE是⊙O的切线,∴∠ODC=∠OEC=∠DCE=90°,∴四边形ODCE是矩形.
∵OD=OE,∴矩形ODCE是正方形,即OE=OD=CD=r,则AD=AF=b﹣r.
连接OB,OF,由勾股定理得:BF2=OB2﹣OF2,BE2=OB2﹣OE2.∵OB=OB,OF=OE,∴BF=BE,则BA+AF=BC+CE,c+b﹣r=a+r,即r=![]() .
.
故选C.
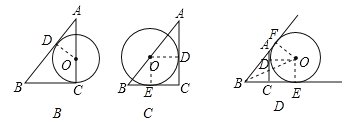


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】青岛、大连两个城市各有机床12台和6台,现将这些机床运往海南10台和厦门8台,每台费用如表一:
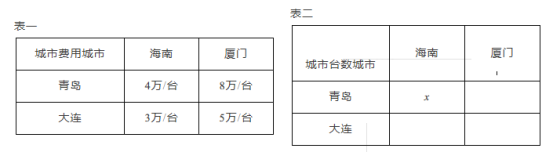
问题1:如表二,假设从青岛运往海南![]() 台机床,并且从青岛、大连运往海南机床共花费36万元,求青岛运往海南机床台数.
台机床,并且从青岛、大连运往海南机床共花费36万元,求青岛运往海南机床台数.
问题2:在问题1的基础上,问从青岛、大连运往海南、厦门的总费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=ax+b与反比例函数y=﹣![]() 的图象交于A(﹣4,1)、B(m,﹣4),且直线l与y轴交于点C.
的图象交于A(﹣4,1)、B(m,﹣4),且直线l与y轴交于点C.
(1)求直线l的解析式;
(2)若不等式ax+b>﹣![]() 成立,则x的取值范围是 ;
成立,则x的取值范围是 ;
(3)若直线x=n(n<0)与y轴平行,且与双曲线交于点D,与直线l交于点H,连接OD、OH、OA,当△ODH的面积是△OAC面积的一半时,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 观察下列三行数:
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
如图,第一行数的第n(n为正整数)个数![]() 用来表示,第二行数的第n个数用
用来表示,第二行数的第n个数用![]() 来表示,第三行数的第n个数用
来表示,第三行数的第n个数用![]() 来表示
来表示
(1)根据你发现的规律,请用含n的代数式表示数![]() ,
,![]() ,
,![]() 的值
的值![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
(2)取每行的第6个数,计算这三个数的和
(3)若![]() 记为x,求
记为x,求![]() (结果用含x的式子表示并化简)
(结果用含x的式子表示并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式![]() ,次数是b,3a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
,次数是b,3a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
![]() 数轴上A、B之间的距离记作
数轴上A、B之间的距离记作![]() ,定义:
,定义:![]() 设点C在数轴上对应的数为x,当
设点C在数轴上对应的数为x,当![]() 时,直接写出x的值.
时,直接写出x的值.
![]() 有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度
有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度![]() 按照如此规律不断地左右运动,当运动了2019次时,求点P所对应的有理数.
按照如此规律不断地左右运动,当运动了2019次时,求点P所对应的有理数.
![]()
![]() 若小蚂蚁甲从点A处以1个单位长度
若小蚂蚁甲从点A处以1个单位长度![]() 秒的速度向左运动,同时小蚂蚁乙从点B处以2单位长度
秒的速度向左运动,同时小蚂蚁乙从点B处以2单位长度![]() 秒的速度也向左运动,一同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
秒的速度也向左运动,一同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
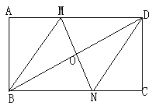
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com