
【题目】青岛、大连两个城市各有机床12台和6台,现将这些机床运往海南10台和厦门8台,每台费用如表一:
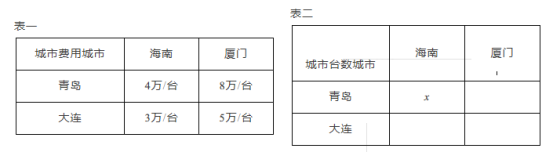
问题1:如表二,假设从青岛运往海南![]() 台机床,并且从青岛、大连运往海南机床共花费36万元,求青岛运往海南机床台数.
台机床,并且从青岛、大连运往海南机床共花费36万元,求青岛运往海南机床台数.
问题2:在问题1的基础上,问从青岛、大连运往海南、厦门的总费用为多少万元?
【答案】问题1:青岛运往海南机床台数是4台;问题2:从青岛、大连运往海南、厦门的总费用为94万元.
【解析】
(1)假设从青岛运往海南x台机床,则从大连运往海南的就是10-x台,根据等量关系:“运往海南机床共花费36万元”,即可列出方程解决问题;
(2)根据问题1中求出的分别从青岛和大连运出的台数,则它们剩下的台数都要运到厦门,由此利用乘法和加法的意义即可解答问题.
(1)设从青岛运往海南x台机床,则从大连运往海南的就是10-x台,根据题意可得方程:
4x+3(10-x)=36,
4x+30-3x=36,
x=6,
则从大连运往海南的有:10-6=4(台).
答:从青岛运往海南6台,从大连运往海南4台.
(2)根据上面计算结果可知:青岛剩下12-6=6(台);大连剩下6-4=2(台),
剩下的这些都要运往厦门,所以需要的费用是:
6×8+2×5,
=48+10,
=58(万元),
36+58=94(万元).
答:从青岛、大连运往海南、厦门的总费用为94万元.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至![]() 处,
处,![]() 与CE交于点F,若∠B=52°,∠DAE=20°,则
与CE交于点F,若∠B=52°,∠DAE=20°,则![]() 的度数为( )
的度数为( )
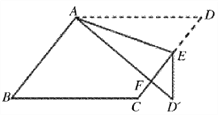
A. 40° B. 36° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
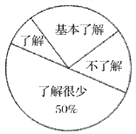
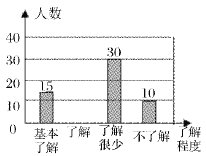
【题目】“食品安全”受到全社会的广泛关注,我市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
扇形统计图 条形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
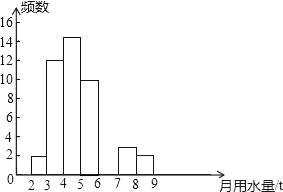
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
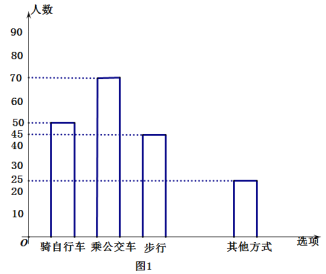
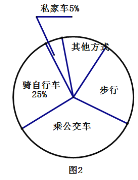
【题目】绿色出行是相对环保的出行方式,通过碳减排和碳中和实现环境资源的可持续利用和交通可持续发展.汽车工业的发展为人类带来了快捷和方便,但同时,汽车的发展也引起了能源的消耗和空气的污染.并且已成为全国各大城市的第一大污染源。实验中学为了解全校学生的交通方式,责成该校七年级(1班)的4位同学对该校部分学生进行了随机调查,按“骑自行车”、“乘公交车”、“步行”、“乘私家车”、“其他方式”设置选项.要求被调查的所有学生从中选一项,并将调查结果绘制成了条形统计图1和扇形统计图2.根据所提供的信息,解答下列问题.
(1)本次调查的人数共有___________人,扇形中步行的圆心角度度数为________.
(2)把条形统计图补充完整.
(3)若该校共有学生3000人,则全校步行的学生大约有多少人数?
(4)根据调查结果对学生的环保出行提一条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=36°.
(1)作∠ABC的平分线BD,交AC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,比较线段DA与BC的大小关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 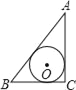 B.
B. 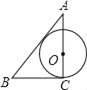 C.
C. 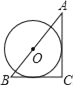 D.
D. 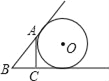
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com