
����Ŀ����֪�����ϣ���OΪԭ�㣬��A��Ӧ����Ϊ9����B��Ӧ����Ϊb����C�ڵ�B�Ҳ࣬����Ϊ2����λ���߶�BC���������ƶ���
![]()
��1����ͼ�����߶�BC��O��A����֮���ƶ���ijһλ��ʱ��ǡ�������߶�AC��OB�����ʱb��ֵ��
��2�����߶�BC��������������AO�����ƶ��Ĺ����У�������AC��OB��![]() AB�����ʱ����������b��ֵ��
AB�����ʱ����������b��ֵ��
��3�����߶�BC���������ƶ�ʱ�������ϵʽ|AC��OB|��![]() |AB��OC|�����ʱb��ȡֵ��Χ���� ��
|AB��OC|�����ʱb��ȡֵ��Χ���� ��
���𰸡���1��3.5����2��![]() ��12����3��b����2��b��9��b��3.5
��12����3��b����2��b��9��b��3.5
��������
��1���������֪B���ʾ�����ȵ�C��Ӧ������2����һ����b��ʾ��AC��OB֮��ľ��룬�����������b����ֵ���ɣ�
��2���ֱ���b��ʾ��AC��OB��AB����һ������AC��0B��![]() AB����������ô𰸼��ɣ�
AB����������ô𰸼��ɣ�
��3���ֱ���b��ʾ��AC��OB��AB��OC����һ������|AC��OB|��![]() |AB��OC|����������ô𰸼��ɣ�
|AB��OC|����������ô𰸼��ɣ�
�⣺��1��������ã�
9����b+2����b��
��ã�b��3.5��
���߶�AC��OB����ʱb��ֵ��3.5��
��2��������ã�
��9����b+2����b��![]() ��9��b����
��9��b����
��ã�b��![]() ��
��
��9����b+2��+b��![]() ��9��b����
��9��b����
��ã�b����12
����AC��0B��![]() AB������������bֵ��
AB������������bֵ��![]() ��12��
��12��
��3���ٵ�b��9ʱ��AC��b+2��9��OB��b��AB��b��9��OC��b+2��
|AC��OB|��![]() |AB��OC|��
|AB��OC|��
|b+2��9��b|��7��
![]() |AB��OC|��
|AB��OC|��![]() ��11��7��
��11��7��
��������
��7��b��9ʱ��
|AC��OB|��![]() |AB��OC|��
|AB��OC|��
|b+2��9��b|��![]() |9��b����b+2��|��
|9��b����b+2��|��
���b����2����ȥ����b��9����ȥ����
��0��b��7ʱ��
|AC��OB|��![]() |AB��OC|��
|AB��OC|��
|9����b+2����b|��![]() |9��b����b+2��|��
|9��b����b+2��|��
���b��![]() ��3.5��
��3.5��
�ܩ�2��b��0ʱ��
|9����b+2��+b|��![]() |9��b����b+2��|��
|9��b����b+2��|��
���b����2��b��9����ȥ����
�ݵ�b����2ʱ��
|9����b+2��+b|��![]() |9��b+��b+2��|�������
|9��b+��b+2��|�������
���ϣ�b��ȡֵ��Χ��b����2��b��9��b��3.5��
�ʴ�Ϊ��b����2��b��9��b��3.5��


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����Ͱ������Բ����Ƭ��һ����������Ƭ�����ף���Ͱ���쳧�IJ��ϳ�����Ҫ����ӹ���Ͱ�õ�Բ����Ƭ�ͳ�������Ƭ�����ϳ����й���42�ˣ�ÿ������ƽ��ÿСʱ���Լӹ�Բ����Ƭ12Ƭ���߳�������Ƭ8Ƭ�����ӳ��为���Ʒ���ӣ�ÿ������ƽ��ÿСʱ���Ժ�����Ͱ9����

��1��������Dz��ϳ������Σ�����ô���乤�˵Ĺ�����
��2��������������ú��ӳ���Ĺ��������ȽϿ�ѧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�����������������е�һ�����⣮ԭ���ǣ����гط�һ�ɣ����������룬��ˮ�ߣ����縰�������밶����ˮ��糤���������Ĵ����ǣ���ͼ����һ��ˮ�أ�ˮ����һ���߳�Ϊ10�ߵ������Σ���ˮ����������һ��«έ�����߳�ˮ��1�ߣ���������«έ����ˮ�رߵ��е㣬���Ķ���ǡ�õ���رߵ�ˮ�森��ˮ����������«έ�ij��ȷֱ��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���ѧϰС����̽�����ε���ֽ����ʱ����һ��ֱ�����ǰ��ֱ�Ƕ����ƾ���ABCD(AB��BC)�ĶԽ��ߵĽ���O��ת(�١��ڡ���)��ͼ�е�M��N�ֱ�Ϊֱ�������ε�ֱ�DZ������ABCD�ı�CD��BC�Ľ��㣮
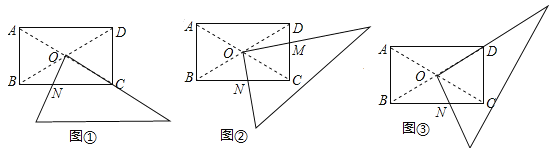
(1)��ѧϰС���Ա����ķ���ͼ����(���ǰ�һ����CC�غ�)��BN��CN��CD�������߶�֮�����һ����������ϵ��CN2��BN2+CD2�������������Ա��ͼ���з��ֵĽ���˵�����ɣ�
(2)��ͼ����(���ǰ�һֱ�DZ���OD�غ�)����̽��ͼ����BN��CN��CD�������߶�֮���������ϵ��ֱ��д����Ľ��ۣ�
(3)��̽��ͼ����BN��CN��CM��DM�������߶�֮���������ϵ��д����Ľ��ۣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ����λ��Ȼ������������������λ�ϣ��ұ���λ�ϵ����ܱ������λ������1����ô���ǰ���������Ȼ���������������������磺234��4567��56789�������ǡ�����������
��1����ֱ��д��������λ��������������С����λ�������������������ǵIJ
��2����ij������������ǡ�õ������λ����469���������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ�����ͼ����A��3��3����B��4��0����ԭ��O��PΪ���κ���ͼ���ϵ�һ�����㣬����P��x��Ĵ��ߣ�����ΪD��m��0��������ֱ��OA���ڵ�C��
��1����ֱ��OA�Ͷ��κ����Ľ���ʽ��
��2������P��ֱ��OA���Ϸ�ʱ��
�ٵ�PC�ij����ʱ�����P�����ꣻ
�ڵ�S��PCO=S��CDOʱ�����P�����꣮
 ��������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣨�����
��һ���㣨�����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ����������
����������![]() ������
������![]() .
.
��1����ͼ1������![]() ���߶�
���߶�![]() ��ʱ����ֱ��д����
��ʱ����ֱ��д����![]() ��
��![]() ��
��![]() �����߶�֮���������ϵΪ________.
�����߶�֮���������ϵΪ________.
��2����ͼ2������![]() ���߶�
���߶�![]() ���ӳ�����ʱ��������������.��1���еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�Ľ��ۣ�������֤��.
���ӳ�����ʱ��������������.��1���еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�Ľ��ۣ�������֤��.
��3����ͼ3������![]() ���߶�
���߶�![]() �ķ����ӳ�����ʱ���ҵ�
�ķ����ӳ�����ʱ���ҵ�![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() �����࣬������������.��ֱ��д����
�����࣬������������.��ֱ��д����![]() ��
��![]() ��
��![]() �����߶�֮���������ϵ______________.
�����߶�֮���������ϵ______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,��ABCD��,�ֱ���AB,ADΪ���������ȱ���ABE,��ADF,�ӳ�CB��AE�ڵ�G,��G�ڵ�A,E֮��,����CG,CF,�����н��۲�һ����ȷ����(��)

A. ��CDF�ա�EBC
B. ��CDF=��EAF
C. CG��AE
D. ��ECF�ǵȱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��E��������ABCD�ĶԽ���AC��,��EC=2AE,ֱ��������FEG����ֱ�DZ�EF��EG�ֱ�BC��DC�ڵ�M��N.��������ABCD�ı߳�Ϊ6,���ص������ı���EMCN�����Ϊ( )
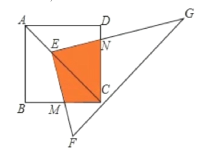
A. 9B. 12C. 16D. 32
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com