
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
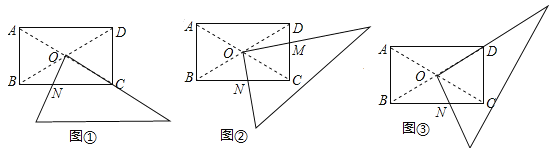
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;
(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.
(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
【答案】(1)见解析;(2)BN2=NC2+CD2;(3)CM2+CN2=DM2+BN2,理由见解析.
【解析】
(1)连结AN,由矩形知AO=CO,∠ABN=90°,AB=CD,结合ON⊥AC得NA=NC,由∠ABN=90°知NA2=BN2+AB2,从而得证;
(2)连接DN,在Rt△CDN中,根据勾股定理可得:ND2=NC2+CD2,再根据ON垂直平分BD,可得:BN=DN,从而可证:BN2=NC2+CD2;
(3)延长MO交AB于点E,可证:△BEO≌△DMO,NE=NM,在Rt△BEN和Rt△MCN中,根据勾股定理和对应边相等,可证:CN2+CM2=DM2+BN2.
(1)证明:连结AN,
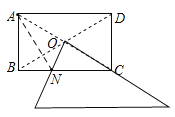
∵矩形ABCD
∴AO=CO,∠ABN=90°,AB=CD,
∵ON⊥AC,
∴NA=NC,
∵∠ABN=90°,
∴NA2=BN2+AB2,
∴NC2=BN2+CD2.
(2)如图2,连接DN.
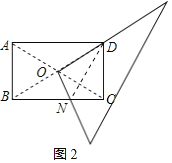
∵四边形ABCD是矩形,
∴BO=DO,∠DCN=90°,
∵ON⊥BD,
∴NB=ND,
∵∠DCN=90°,
∴ND2=NC2+CD2,
∴BN2=NC2+CD2.
(3)CM2+CN2=DM2+BN2
理由如下:延长MO交AB于E,
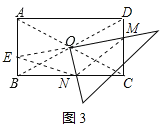
∵矩形ABCD,
∴BO=DO,∠ABC=∠DCB=90°,AB∥CD,
∴∠ABO=∠CDO,∠BEO=∠DMO,
∴△BEO≌△DMO(ASA),
∴OE=OM,BE=DM,
∵MO⊥EM,
∴NE=NM,
∵∠ABC=∠DCB=90°,
∴NE2=BE2+BN2,NM2=CN2+CM2,
∴CN2+CM2=BE2+BN2,
即CN2+CM2=DM2+BN2.


科目:初中数学 来源: 题型:
【题目】网上购买鞋子时,消费者需要根据自己脚的情况选择合适的鞋码,每个人千差万别,我们常常会看到下面的表格帮助我们选购:
表1 脚长脚码对应表
脚长(mm) | 220 | 225 | 230 | 235 | 240 | 245 | 250 | 255 | 260 | 265 |
鞋码 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
其中脚长的测量方法是:将脚轻踏于白纸上,在脚趾最长处确定一点,在脚后跟确定一点,测量两点之间的距离,如下图所示
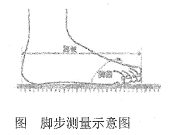
如果一名运动员的脚长是273mm,按上述脚长脚码对应关系他应该穿_________码的鞋子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
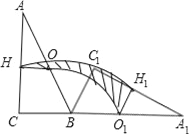
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学参加社会实践活动,到“庐江台湾农民创业园”了解大棚蔬菜生长情况.他们分两组对西红柿的长势进行观察测量,分别收集到10株西红柿的高度,记录如下(单位:厘米)
第一组:32 39 45 55 60 54 60 28 56 41
第二组:51 56 44 46 40 53 37 47 50 46
根据以上数据,回答下列问题:
(1)第一组这10株西红柿高度的平均数是 ,中位数是 ,众数是 .
(2)小明同学计算出第一组方差为S12=122.2,请你计算第二组方差,并说明哪一组西红柿长势比较整齐.
查看答案和解析>>
科目:初中数学 来源: 题型:
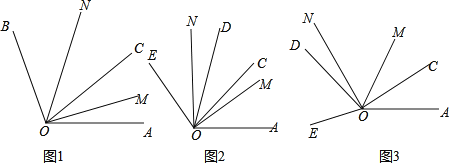
【题目】(1)如图1,∠AOC=α,∠BOC=β,若OM平分∠AOC,ON平分∠BOC,则∠MON= (用含α、β的式子表示);
(2)如图2,若将∠BOC绕点O逆时针旋转30°后得到∠EOD,OM平分∠AOD,ON平分∠COE,求∠MON的度数(用含α、β的式子表示);
(3)若∠BOC旋转90°至图3的位置,其他条件不变,则∠MON的度数是 (用含α、β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点O为原点,点A对应的数为9,点B对应的数为b,点C在点B右侧,长度为2个单位的线段BC在数轴上移动.
![]()
(1)如图,当线段BC在O、A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)当线段BC在数轴上沿射线AO方向移动的过程中,若存在AC﹣OB=![]() AB,求此时满足条件的b的值;
AB,求此时满足条件的b的值;
(3)当线段BC在数轴上移动时,满足关系式|AC﹣OB|=![]() |AB﹣OC|,则此时b的取值范围是
|AB﹣OC|,则此时b的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“弘扬柳乡工匠精神,共筑乡村振兴之梦”第三届柳编文化节暨首届“襄阳人游襄州”启动仪式在浩然广场举行。为了迎接此次盛会,某工艺品厂柳编车间组织![]() 名工人赶制一批柳编工艺品,为了解每名工人的日均生产能力,随机调查了某天每个工人的生产件数,获得数据如下表:
名工人赶制一批柳编工艺品,为了解每名工人的日均生产能力,随机调查了某天每个工人的生产件数,获得数据如下表:

则这一天![]() 名工人生产件数的众数和中位数分别是( )
名工人生产件数的众数和中位数分别是( )
A. ![]() 件、
件、![]() 件B.
件B. ![]() 件、
件、![]() 件C.
件C. ![]() 件、
件、![]() 件D.
件D. ![]() 件、
件、![]() 件
件
查看答案和解析>>
科目:初中数学 来源: 题型:
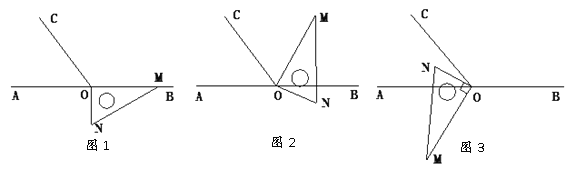
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com