
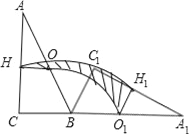
【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】出租车司机沿东西方向的公路送旅客,如果约定向东为正,向西为负,当天的历史记录如下(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)出租车司机最后到达的地方在出发点的哪个方向?距出发点多远?
(2)出租车司机最远离出发点有多远?
(3)若汽车每千米耗油量为![]() 升,则这天共耗油多少升?
升,则这天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,油桶制造厂的裁料车间主要负责加工油桶用的圆形铁片和长方形铁片,裁料车间有工人42人,每个工人平均每小时可以加工圆形铁片12片或者长方形铁片8片;焊接车间负责成品焊接,每个工人平均每小时可以焊接油桶9个.

(1)如果你是裁料车间主任,你怎么分配工人的工作?
(2)你觉得怎样配置焊接车间的工人数量比较科学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司2017年10月份销售一种新型低能耗汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆.
(1)求11月份和12月份的平均增长率;
(2)该型号汽车每辆的进价为10万元,且销售a辆汽车,汽车厂队销售公司每辆返利0.03a万元,该公司这种型号汽车的售价为11万元/辆,若使2018年1月份每辆汽车盈利不低于2.6万元,那么该公司1月份至少需要销售该型号汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016青海省西宁市)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
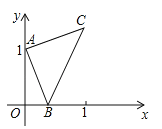
A.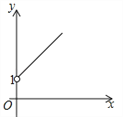 B.
B.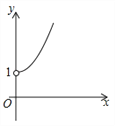 C.
C.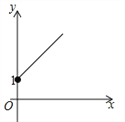 D.
D.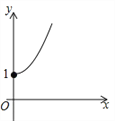
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
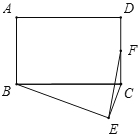
A. 8B. 9C. 10D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
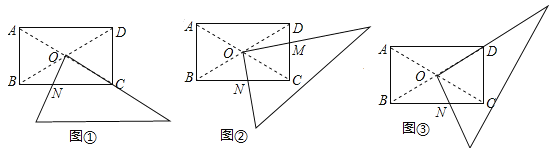
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;
(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.
(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )

A. △CDF≌△EBC
B. ∠CDF=∠EAF
C. CG⊥AE
D. △ECF是等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com