
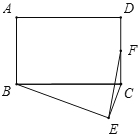
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A. 8B. 9C. 10D. 2![]()
【答案】B
【解析】
取BC中点O,连接OE,OF,根据矩形的性质可求OC,CF的长,根据勾股定理可求OF的长,根据直角三角形的性质可求OE的长,根据三角形三边关系可求得当点O,点E,点F共线时,EF有最大值,即EF=OE+OF.
解:如图,取BC中点O,连接OE,OF,
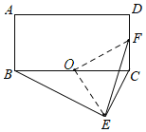
∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠C=90°,
∵点F是CD中点,点O是BC的中点,
∴CF=3,CO=4,
∴OF=![]() =5,
=5,
∵点O是Rt△BCE的斜边BC的中点,
∴OE=OC=4,
∵根据三角形三边关系可得:OE+OF≥EF,
∴当点O,点E,点F共线时,EF最大值为OE+OF=4+5=9.
故选:B.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
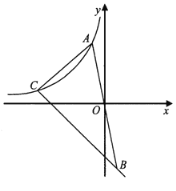
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
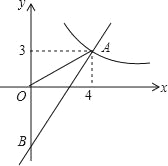
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点都在格点上.
⑴ 在线段AC上找一点P(不能借助圆规),使得![]() ,画出点P的位置,并说明理由.
,画出点P的位置,并说明理由.
⑵ 求出⑴中线段PA的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
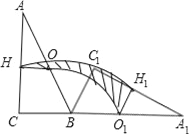
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富课外活动,某校将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付款.
某校要到该商场购买乒乓球拍20副,乒乓球![]() 盒(
盒(![]() >20且为整数).
>20且为整数).
(1)若按方案一购买,需付款 元(用含![]() 的整式表示,要化简); 若按方案二购买,需付款 元(用含
的整式表示,要化简); 若按方案二购买,需付款 元(用含![]() 的整式表示,要化简).
的整式表示,要化简).
(2)若![]() 30,通过计算说明此时按哪种方案购买较为合算?
30,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() 30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学参加社会实践活动,到“庐江台湾农民创业园”了解大棚蔬菜生长情况.他们分两组对西红柿的长势进行观察测量,分别收集到10株西红柿的高度,记录如下(单位:厘米)
第一组:32 39 45 55 60 54 60 28 56 41
第二组:51 56 44 46 40 53 37 47 50 46
根据以上数据,回答下列问题:
(1)第一组这10株西红柿高度的平均数是 ,中位数是 ,众数是 .
(2)小明同学计算出第一组方差为S12=122.2,请你计算第二组方差,并说明哪一组西红柿长势比较整齐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
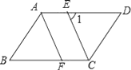
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com