【题目】如图，在正方形网格中，每个小正方形的边长为1个单位长度．△ABC的三个顶点都在格点上.
⑴ 在线段AC上找一点P（不能借助圆规），使得
，画出点P的位置，并说明理由．
⑵ 求出⑴中线段PA的长度.
【答案】(1)详见解析；（2）线段PA的长度为
.
【解析】试题分析：
（1）利用方格纸可作出BC的垂直平分线交AC于点P，点P为所求的点，由线段垂直平分线的性质和勾股定理即可证明此时：PC2-PA2=AB2；
（2）由图中信息可得AB=4，AC=6，设PA= 
，则PC=PB=6- 
，在Rt△PAB中，由勾股定理建立方程解出
即可.
试题解析：
⑴ 如图，利用方格纸作BC的垂直平分线，分别交AC、BC于点P、Q，则PC＝PB.
∵在△APB中，∠A＝90°，
∴
，即： 
，
∴
.
⑵ 由图可得：AC=6，AB=4，设PA=x，则PB=PC=6－x
∵在△PAB中，∠A＝90°，
∴
，解得： 
，即PA=
.
答：线段PA的长度为
.
能考试期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】若干个工人装卸一批货物，每个工人的装卸速度相同，如果这些工人同时工作，则需10小时装卸完毕；现改变装卸方式，开始一个人干，以后每隔t（整数）小时增加一个人干，每个参加装卸的人都一直干到装卸完毕，且最后参加的一个人装卸的时间是第一个人的
，则按改变的方式装卸，自始至终共需时间_____小时．
查看答案和解析>>
科目：初中数学 来源： 题型：
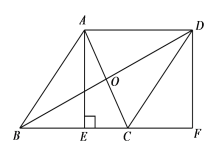
【题目】如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF=BE，连接DF．
（1）求证：四边形AEFD是矩形；
（2）若AC=4，∠ABC=60°，求矩形AEFD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，是由一些大小相同的小正方体组合成的简单几何体，并放在墙角．（注：图3、图4、图5每一个小方格的边长为1cm）
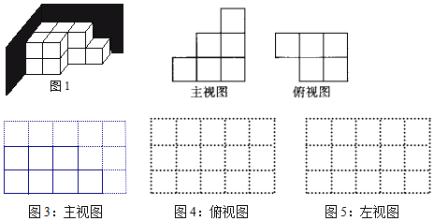
（1）该几何体主视图如图3所示，请在图4方格纸中画出它的俯视图；
（2）若将其露在外面的表面涂一层漆，则其涂漆面积为 cm2．（正方体的棱长为1cm）
（3）用一些小立方块搭一个几何体，使它的主视图和俯视图如图所示，它最少需要多少个小立方块？最多需要多少个小立方块？并在图5方格纸中画出需要最多小立方块的几何体的左视图．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某汽车销售公司2017年10月份销售一种新型低能耗汽车20辆，由于该型号汽车经济适用性强，销量快速上升，12月份该公司销售该型号汽车达45辆．
（1）求11月份和12月份的平均增长率；
（2）该型号汽车每辆的进价为10万元，且销售a辆汽车，汽车厂队销售公司每辆返利0.03a万元，该公司这种型号汽车的售价为11万元/辆，若使2018年1月份每辆汽车盈利不低于2.6万元，那么该公司1月份至少需要销售该型号汽车多少辆？此时总盈利至少是多少万元？（盈利＝销售利润+返利）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．
(1)求证：△ACE≌△BCD；
(2)若AD＝5，BD＝12，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB＝6，AD＝8，以BC为斜边在矩形的外部作直角三角形BEC，点F是CD的中点，则EF的最大值为( )
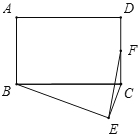
A. 8B. 9C. 10D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校运动会4×100米是最精彩的比赛项目，下表是七年级1班与2班在比赛时各运动员的接棒时间（假设每名运动员跑步速度不变，交接棒时间忽路不计，每名运动员都恰好跑100m，两个班级均用了55秒的时间达到终点（单位：秒）：
班级 | 第二棒接棒时间 | 第三棒接棒时间 | 第四棒接棒时间 |
1班 | 12 | 28 | 40 |
2班 | 13 | 25 | 41 |
（1）两个班级共八名学生中跑的最慢的学生跑完100米用的时间是 秒；
（2）当2班第二棒运动员接棒时，1班运动员领先 米；
（3）求从出发开始计时，多长时间两队第一次并列？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
