
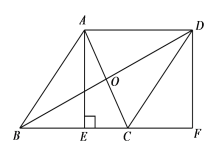
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)若AC=4,∠ABC=60°,求矩形AEFD的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据已知条件推知四边形AEFD是平行四边形,AE⊥BC,则平行四边形AEFD是矩形;
(2)先证明△ABE≌△DCF,得出△ABC是等边三角形,在利用面积公式列式计算即可得解.
(1)证明: ∵ 菱形ABCD
∴AD∥BC , AD=BC
∵CF=BE
∴BC=EF
∴AD∥EF,AD=EF
∴四边形AEFD是平行四边形
∵AE⊥BC
∴∠AEF=90°
∴平行四边形AEFD是矩形
(2)根据题意可知∠ABE=∠DCF,AB=CD,CF=BE
∴△ABE≌△DCF (SAS)
∴矩形AEFD的面积=菱形ABCD的面积
∵∠ABC=60°,∴△ABC是等边三角形
AC=4,AO=2,AB=4,由菱形的对角线互相垂直可得BO=![]()
矩形AEFD的面积=菱形ABCD的面积=![]()


科目:初中数学 来源: 题型:
【题目】某自主服装品牌设计出了一种西装和领带,西装每套定价200元,领带每条定价40元.在推广服装品牌初期开展促销活动,可以同时向客户提供两种优惠方案:
方案①买一套西装送一条领带;
方案②西装和领带都按定价的90%付款.
现某客户要到该服装品牌购买西装20套,领带![]() 条(
条(![]() 超过20).
超过20).
(1)若该客户按方案①购买,需付款_ _____元(用含![]() 的式子表示);
的式子表示);
若该客户按方案②购买,需付款__ ____元(用含![]() 的式子表示);
的式子表示);
(2)若![]() =30,通过计算说明此时按哪种方案购买较为合算?
=30,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() =30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
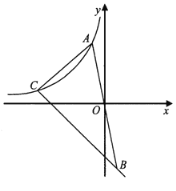
【题目】如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
拆项法是因式分解中一种技巧较强的方法,它通常是把多项式中的某一项拆成几项,再分组分解,因而有时需要多次实验才能成功,例如把![]() 分解因式,这是一个三项式,最高次项是三次项,一次项系数为零,本题既没有公因式可提取,又不能直接应用公式,因而考虑制造分组分解的条件,把常数项拆成1和3,原式就变成
分解因式,这是一个三项式,最高次项是三次项,一次项系数为零,本题既没有公因式可提取,又不能直接应用公式,因而考虑制造分组分解的条件,把常数项拆成1和3,原式就变成![]() ,再利用立方和与平方差先分解,解法如下:
,再利用立方和与平方差先分解,解法如下:
原式![]()
![]()
公式:![]() ,
,![]()
根据上述论法和解法,
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)因式分解:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购买鞋子时,消费者需要根据自己脚的情况选择合适的鞋码,每个人千差万别,我们常常会看到下面的表格帮助我们选购:
表1 脚长脚码对应表
脚长(mm) | 220 | 225 | 230 | 235 | 240 | 245 | 250 | 255 | 260 | 265 |
鞋码 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
其中脚长的测量方法是:将脚轻踏于白纸上,在脚趾最长处确定一点,在脚后跟确定一点,测量两点之间的距离,如下图所示
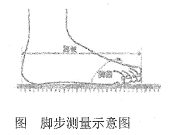
如果一名运动员的脚长是273mm,按上述脚长脚码对应关系他应该穿_________码的鞋子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),
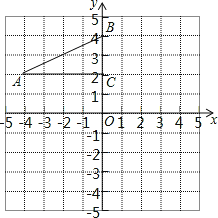
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
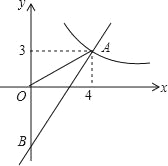
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点都在格点上.
⑴ 在线段AC上找一点P(不能借助圆规),使得![]() ,画出点P的位置,并说明理由.
,画出点P的位置,并说明理由.
⑵ 求出⑴中线段PA的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com