
����Ŀ��ij������װƷ����Ƴ���һ����װ���������װÿ����200Ԫ�����ÿ������40Ԫ�����ƹ��װƷ�Ƴ��ڿ�չ�����������ͬʱ��ͻ��ṩ�����Żݷ�����
��������һ����װ��һ�������
��������װ������������۵�90%���
��ij�ͻ�Ҫ���÷�װƷ�ƹ�����װ20�ף����![]() ����
����![]() ����20����
����20����
��1�����ÿͻ��������������踶��_ _____Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
���ÿͻ��������������踶��__ ____Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����![]() =30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
=30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3����![]() =30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
=30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
���𰸡���1����40x+3200������36x+3600����2��������һ������㣨3��4360Ԫ
�������������������1���������ַ�����Ҫ��ֱ��ʾ�����ַ�����Ӧ������������2����x=30ʱ���ֱ��������ַ�����Ӧ���������Ƚϼ��ɽ����������3���ɰ����ָ��ʽ�ۺ���һ�𣬼�������һ����20����װ����20���������10�������������������360Ԫ���ټ�������ü���.
���������
��1������һ��20��200+40��x-20��=40x+3200��
����������20��200+40x����90%=36x+3600��
�ʴ�Ϊ��40x+3200������36x+3600����
��2����x=30ʱ������һ��40x+3200=40��30+3200=4400Ԫ��
��������36x+3600=36��30+3600=4680Ԫ��
��4400Ԫ��4680Ԫ����������һ������㣻
��3���Ȱ�����һ����20����װ����20���������10�������������������360Ԫ��
������20��200+40��10��90%=4360Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
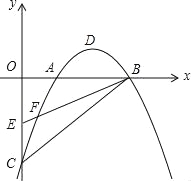
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��2��a��0����x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C���䶥��Ϊ��D����E������Ϊ��0����1��������������BE������һ��F������BC��
��1����������ߵĽ���ʽ�������䷽���ѽ���ʽ��Ϊy=a��x��h��2+k����ʽ��
��2������H��1��y����BC�ϣ�����FH�����FHB�������
��3��һ����M�ӵ�D��������ÿ��1����λ���ٶ�ƽ������y�᷽�������˶�������OM��BM�����˶�ʱ��Ϊt�루t��0�����ڵ�M���˶������У���tΪ��ֵʱ����OMB=90�㣿
��4����x���Ϸ����������ϣ��Ƿ���ڵ�P��ʹ�á�PBF��BAƽ�֣������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c������ABC���������㣬��y���ཻ�ڣ�0��![]() ������A����Ϊ����1��2������B�ǵ�A����y��ĶԳƵ㣬��C��x����������ϣ�
������A����Ϊ����1��2������B�ǵ�A����y��ĶԳƵ㣬��C��x����������ϣ�
��1����������ߵĺ�����ϵ����ʽ��
��2����FΪ�߶�AC��һ���㣬��F��FE��x�ᣬFG��y�ᣬ����ֱ�ΪE��G�����ı���OEFGΪ������ʱ�����F������꣮
��3������2���е�������OEFG��OC����ƽ�ƣ���ƽ���е�������OEFGΪ������DEFG������E�͵�C�غ�ʱֹͣ�˶�����ƽ�Ƶľ���Ϊt�������εı�EF��AC���ڵ�M��DG���ڵ�ֱ����AC���ڵ�N������DM���Ƿ����������t��ʹ��DMN�ǵ��������Σ������ڣ���t��ֵ������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�Сӱ��С÷���ܵ�·��s(��)������ʱ��t(��)֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD������˵����ȷ���ǣ� ��
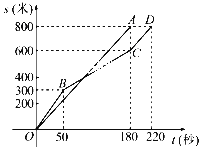
A. Сӱ���ٶ���ʱ������������
B. С÷���ٶ���ʱ����������С
C. �����ܺ�180��ʱ����������
D. �����ܺ�50��ʱ��С÷��Сӱ��ǰ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=��2x+1��ͼ���������ĸ�����(����)
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
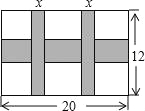
����Ŀ��һ����20cm����12cm��ͼ������ͼ��������һ�������IJ������ᡢ�������Ŀ��ȱ�Ϊ3��2�����������Ŀ���Ϊxcm��ͼ��������������ռ���Ϊycm2��
��1����y��x֮��ĺ�����ϵʽ��
��2����ͼ��������������ռ�����ͼ�������![]() ����ᡢ�������Ŀ��ȣ�
����ᡢ�������Ŀ��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�������Ϸֱ��ʾ������a��b����A��ԭ��O����֮��� �����ʾΪAO����AO��|a-0|��|a|�����Ƶأ���B��ԭ��O����֮��ľ����ʾ ΪBO����BO��|b|����A���B����֮��ľ����ʾΪAB��|a-b|.�������ᣬ˼�����ش��������⣺
(1)�������ϱ�ʾ1�ͣ�3������֮��ľ�����__________��
�������ϱ�ʾm�ͣ�1������֮��ľ�����__________��
�������ϱ�ʾm�ͣ�1������֮��ľ�����3����������m��___________��
(2)��x��ʾһ��������������x�ȣ�3��x��1С����|x-1|+|x+3|=______��
(3)������|x-2|+|x+4|=6����������x�ĺ�.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��mx+2m=0��������ȵ�ʵ��������m���ڣ� ��
A.0��8
B.0
C.8
D.2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com