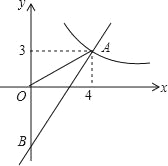
【题目】如图，一次函数y=kx+b的图象分别与反比例函数y=的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．

（1）求函数y=kx+b和y=的表达式；

（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．

参考答案：

【答案】（1）y=， y=2x﹣5；（2）点M的坐标为（2.5，0）．

【解析】（1）利用待定系数法即可解答；

（2）设点M的坐标为（x，2x﹣5），根据MB=MC，得到，即可解答．

（1）把点A（4,3）代入函数y=得：a=3×4=12，∴y=．OA==5，

∵OA=OB，∴OB=5，∴点B的坐标为（0，﹣5），

把B（0，﹣5），A（4，3）代入y=kx+b得：解得：∴y=2x﹣5．

（2）∵点M在一次函数y=2x﹣5上，∴设点M的坐标为（x，2x﹣5），

∵MB=MC，∴

解得：x=2.5，∴点M的坐标为（2.5，0）．

“点睛”本题考查了一次函数与反比例函数的交点，解决本题的关键是利用待定系数法求解析式.

关闭