
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
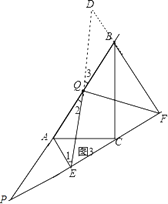
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
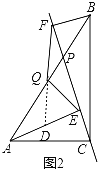
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.

【答案】(1)AE∥BF,QE=QF;(2)QE=QF,证明见试题解析;(3)成立,证明见试题解析.
【解析】试题分析:(1)、证△BFQ≌△AEQ即可;(2)、证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可;(3)、证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可.
试题解析:(1)、AE∥BF,QE=QF, 理由是:如图1,∵Q为AB中点, ∴AQ=BQ,
∵BF⊥CP,AE⊥CP, ∴BF∥AE,∠BFQ=∠AEQ=90°, 在△BFQ和△AEQ中
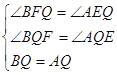 ∴△BFQ≌△AEQ(AAS), ∴QE=QF,
∴△BFQ≌△AEQ(AAS), ∴QE=QF,
(2)、QE=QF, 如图2,延长FQ交AE于D, ∵Q为AB中点, ∴AQ=BQ,
∵BF⊥CP,AE⊥CP, ∴BF∥AE, ∴∠QAD=∠FBQ, 在△FBQ和△DAQ中
 ∴△FBQ≌△DAQ(ASA), ∴QF=QD, ∵AE⊥CP,
∴△FBQ≌△DAQ(ASA), ∴QF=QD, ∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线, ∴QE=QF=QD, 即QE=QF.
(3)、(2)中的结论仍然成立, 如图3, 延长EQ、FB交于D, ∵Q为AB中点,
∴AQ=BQ, ∵BF⊥CP,AE⊥CP, ∴BF∥AE, ∴∠1=∠D, 在△AQE和△BQD中,
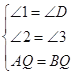 , ∴△AQE≌△BQD(AAS), ∴QE=QD, ∵BF⊥CP,
, ∴△AQE≌△BQD(AAS), ∴QE=QD, ∵BF⊥CP,
∴FQ是斜边DE上的中线, ∴QE=QF.



 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
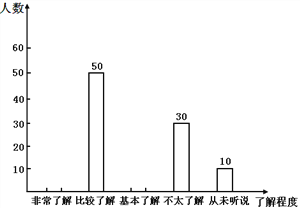
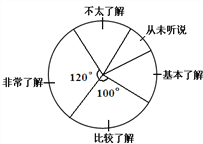
【题目】我区某中学八年级学生对全区中学生“创建国家卫生城市”知晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”、“从未听说”五个等级,统计后的数据绘制成如下所示的不完整的统计图:
(1)本次问卷调查抽取的样本容量为 ,“基本了解”所在扇形的圆心角等于 °;
(2)请你将条形统计图1补充完整;
(3)若我区有5400名中学生,你估计我区可能有多少名中学生不太了解“创建国家卫生城市”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程2y2﹣7=3y的二次项系数、一次项系数、常数项分别是( )
A.2,﹣3,﹣7B.﹣2,﹣3,﹣7C.2,﹣7,3D.﹣2,﹣3,7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com