
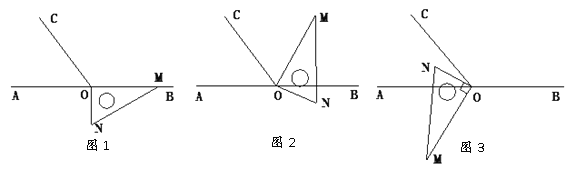
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)平分;(2)(2)t=59或14 (3)∠AOM-∠NOC=220
【解析】
试题(1)根据角平分线的定义和平角的定义求出∠COP=30°,即可证得直线ON平分∠AOC;
(2)当ON绕O点旋转至图②位置时,此时ON转过60°,旋转时间为10秒;当ON转至锐角∠AOC内部平分∠AOC时,ON转过90°+150°=240°,旋转时间为40秒;
(3)根据∠AOM+∠AON=90°,∠AON+∠NOC=60°,得到∠AOM一∠NOC =30°.
试题解析:(1)直线ON平分∠AOC(如图),理由如下:
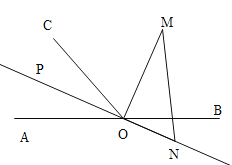
∵OM平分∠BOC,且∠BOC=120°,
∴∠COM=60°,
又∠MON=90°,
∴∠POM=90°,
∴∠COP=30°,
又∠AOC=60°,
∴OP平分∠AOC,
即直线ON平分∠AOC.
(2)当ON绕O点旋转至图②位置时,ON平分∠AOC,此时ON转过60°,
当ON转至锐角∠AOC内部平分∠AOC时,ON转过90°+150°=240°,
所以t=10或40(秒) ,
答:旋转时间t的值为10秒或40秒.
(3) ∠AOM—∠NOC=30°,
∵∠AOM+∠AON=90°,
∠AON+∠NOC=60°,
∴∠AOM一∠NOC =30°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
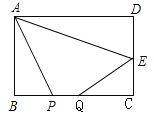
【题目】如图,在矩形ABCD中 ,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为( )
A. 1 B. 2 C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题.
(1)商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商品制定了两种优惠方法:
①买一只茶壶赠一只茶杯;②按总价的90%付款.某顾客购买茶壶5只,茶杯若干只(不少于5只),问顾客买多少只茶杯时,两种方法付款相同.假如该顾客买了茶杯20只,哪种买法实惠?
(2)某人原计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达,但他因事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A,B两地间的距离.
(3)某工厂完成一批产品,一车间单独完成需30天,二车间单独完成需20天.
①如一车间先做若干天,然后由二车间继续做,直至完成,前后共做了25天,问一车间先做了几天?
②如一车间先做了3天后,二车间加入一起做,还需多少天才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为直线AB上一点,将一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板的一边ON与射线OB重合,过点O在三角板的内部,作射线OC,使∠NOC:∠MOC=2:1,求∠AOC的度数;
(2)如图2,将三角板绕点O逆时针旋转一定角度到图2的位置,过点O在三角板MON的内部作射线OC,使得OC恰好是∠MOB对的角平分线,此时∠AOM与∠NOC满足怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
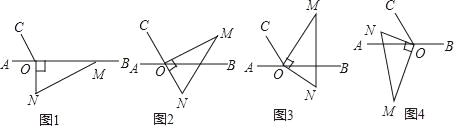
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数;
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB. 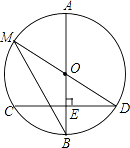
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com