
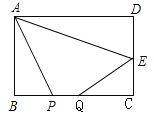
【题目】如图,在矩形ABCD中 ,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为( )
A. 1 B. 2 C. 2![]() D. 4
D. 4
【答案】D
【解析】要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度.
如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.
∵GH=DF=6,EH=2+4=6,∠H=90°,
∴∠GEH=45°.
设BP=x,则CQ=BC-BP-PQ=8-x-2=6-x,
在△CQE中,
∵∠QCE=90°,∠CEQ=45°,
∴CQ=EC,
∴6-x=2,
解得x=4.
故选D.



 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是米.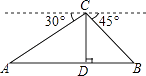
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,CE与BF相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)□ABCD应满足什么条件时,四边形EHFG是矩形?并说明理由;
(3)□ABCD应满足什么条件时,四边形EHFG是正方形?(不要说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
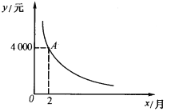
【题目】李先生参加了某电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为1.2万元,交了首付4000元之后每期付款y元,x个月结清余款.
(1)写出y与x的函数关系式.
(2)如打算每月付款不超过500元,李先生至少几个月才能结清余款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)矩形![]() 中,
中,![]() .分别以
.分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图1所示的平面直角坐标系.
轴,建立如图1所示的平面直角坐标系.![]() 是
是![]() 边上一个动点(不与
边上一个动点(不与![]() 重合),过点
重合),过点![]() 的反比例函数y=
的反比例函数y=![]() (
(![]() )的图像与边
)的图像与边![]() 交于点
交于点![]() .
.
(1)当点![]() 运动到边
运动到边![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(2)连接EF、AB,求证:EF∥AB;
(3)如图2,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,求此时反比例函数的解析式.
处,求此时反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的妙点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的妙点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的妙点,但点D是(B,A)的妙点.
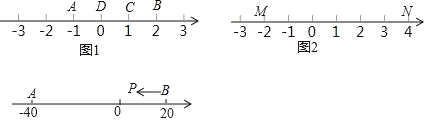
知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
(1)数 所表示的点是(M,N)的妙点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发向左运动,到达点A停止.P点运动多少个单位时,P、A和B中恰有一个点为其余两点的妙点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第6个小房子用的石子数量为 ( )

A. 87 B. 77 C. 70 D. 60
查看答案和解析>>
科目:初中数学 来源: 题型:
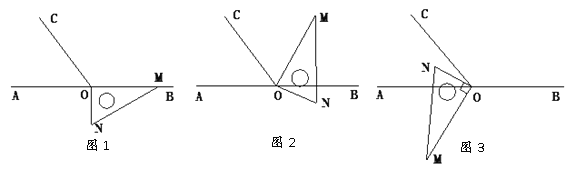
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com