
����Ŀ���Ķ����⣺
��A��B��CΪ���������㣬����C��A�ľ����ǵ�C��B�ľ���2�������ǾͳƵ�C�ǣ�A��B������㣮
���磬��ͼ1����A��ʾ����Ϊ��1����B��ʾ����Ϊ2����ʾ1�ĵ�C����A�ľ�����2������B�ľ�����1����ô��C�ǣ�A��B������㣻���磬��ʾ0�ĵ�D����A�ľ�����1������B�ľ�����2����ô��D�Ͳ��ǣ�A��B������㣬����D�ǣ�B��A������㣮
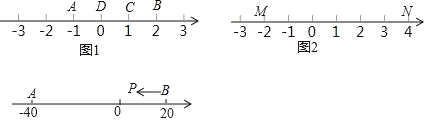
֪ʶ���ã���ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ4��
��1������ ������ʾ�ĵ��ǣ�M��N������㣻
��2����ͼ3��A��BΪ���������㣬��A����ʾ����Ϊ��40����B����ʾ����Ϊ20������һֻ��������P�ӵ�B���������˶��������Aֹͣ��P���˶����ٸ���λʱ��P��A��B��ǡ��һ����Ϊ�����������㣿
���𰸡���1��2��10;��2����������
��������
(1) ��������Ϊx, �����ŵ�Ķ���������M��N֮�������ڵ�N�ұ�,�г����̽ⷽ�̼���;
(2)�������Ķ����֪���������:��PΪ(A, B) �����; ��PΪ (B,A) �����;��BΪ (A, P) �����. AΪ(B��P)��������P��ʾ����Ϊy,�������Ķ����г�����, �����ó���ֵ.
�⣺��1����������Ϊx���������
x������2��=2��4��x����
���x=2��
��x+2=2��x��4����
���x=10��
����2��10����ʾ�ĵ��ǡ�M��N������㣻
�ʴ�Ϊ��2��10��
��2�����P��ʾ����Ϊy�������������
��P�ǡ�A��B������㣮
�����⣬��y������40��=2��20��y����
���y=0��
20��0=20��
��P�ǡ�B��A������㣮
�����⣬��20��y=2[y������40��]��
���y=��20��
20������20��=40��
��B�ǡ�A��P������㣮
�����⣬��20������40��=2��20��y����
���y=��10��
20������10��=30��
��AΪ��B��P������㣬
�������20������40��=2[y������40��]
y=��10��
20������10��=30��
���Ͽ�֪����P���˶�20��40��30����λʱ��P��A��B��ǡ��һ����Ϊ�����������㣮


 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ǡ����ܻ�������ɫ���С���ʶ����ǿ��Խ��Խ�����ϲ�������г����У�Ҳ�����г��̼Ҵ����̻���ij���г��о�Ӫ��A�����г�ȥ�������ܶ�Ϊ8��Ԫ������������г�ÿ���ۼ�Ԥ�Ʊ�ȥ�꽵��200Ԫ�������ͳ�������������ȥ����ͬ����ô����������ܶ��ȥ�����10%����
��1��A�����г�ȥ��ÿ���ۼ۶���Ԫ��
��2���ó��н���ƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ���������������֪��A�ͳ���B�ͳ��Ľ����۸�ֱ�Ϊ1500Ԫ��1800Ԫ���ƻ�B�ͳ����ۼ۸�Ϊ2400Ԫ��Ӧ�����֯��������ʹ�������г����ۻ�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���żҽ���Ϊ������������ˮ����Ҫ����һ��ȫ��Ϊ300����ˮ�ŷŹܵ�������120��Ϊ�˾����ܼ���ʩ���Գ��н�ͨ����ɵ�Ӱ�죬����ÿ��Ĺ�������ԭ�ƻ�����20%�����������27���������һ������ԭ�ƻ�ÿ������ܵ������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������![]() ��ͼ����A(2��4)��B(-4��n)���㣬��x���ڵ�C��
��ͼ����A(2��4)��B(-4��n)���㣬��x���ڵ�C��

(1)��m��n��ֵ��
(2)��ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
(3)��x���·���ͼ����x�ᷭ�ۣ���B���ڵ�B����������AB�䡢B��C������A B��C�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�� ,AB=4��BC=8����EΪCD�е㣬P��QΪBC�����������㣬��PQ=2�����ı���APQE�ܳ���Сʱ��BP�ij�Ϊ�� ��
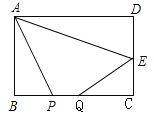
A. 1 B. 2 C. 2![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ķ���x2-(2k+1)x+4k-2=0
�ķ���x2-(2k+1)x+4k-2=0
��1����֤������kȡ��ֵ�������������ʵ����
��2����������ABCһ�߳�a=4�������߳�b��cǡ����������̵�����������ABC���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B���������ϣ�OΪԭ�㣮
��1����B��ʾ������_________________��
��2������B��ÿ��2����λ���ȵ��ٶ������������˶�����2����B��ʾ������________��
��3������A��B�ֱ���ÿ��1����λ���ȡ�3����λ���ȵ��ٶ������������˶�������O������t���A��B��O����������һ����������������Ϊ�˵���߶ε��е㣬��t��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a![]() b���¹涨��һ�����㷨��a
b���¹涨��һ�����㷨��a![]() b=a2+ab������3
b=a2+ab������3![]() ����2��=32+3������2��=3��
����2��=32+3������2��=3��
��1����3��![]() 5��ֵ��
5��ֵ��
��2��������2��![]() x=6����x��ֵ��
x=6����x��ֵ��
��3����3![]() ��2
��2![]() x��=��4+x����x��ֵ��
x��=��4+x����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬A��B��C���������Ϊ�� ![]() ��0������3
��0������3 ![]() ��0������0��5������D�ڵ�һ���ޣ��ҡ�ADB=60�㣬���߶�CD�ij�����СֵΪ ��
��0������0��5������D�ڵ�һ���ޣ��ҡ�ADB=60�㣬���߶�CD�ij�����СֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com