练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】张家界市为了治理城市污水，需要铺设一段全长为300米的污水排放管道，铺设120米后，为了尽可能减少施工对城市交通所造成的影响，后来每天的工作量比原计划增加20%，结果共用了27天完成了这一任务，求原计划每天铺设管道多少米？

    【答案】解：设原计划每天铺设管道x米， 依题意得： ，
    解得x=10，
    经检验，x=10是原方程的解，且符合题意．
    答：原计划每天铺设管道10米
    【解析】设原计划每天铺设管道x米，根据需要铺设一段全长为300米的污水排放管道，铺设120米后，为了尽可能减少施工对城市交通所造成的影响，后来每天的工作量比原计划增加20%，结果共用了27天完成了这一任务，根据等量关系：铺设120米管道的时间+铺设（300﹣120）米管道的时间=27天，可列方程求解．
    【考点精析】解答此题的关键在于理解分式方程的应用的相关知识，掌握列分式方程解应用题的步骤：审题、设未知数、找相等关系列方程、解方程并验根、写出答案（要有单位）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，点C为AB延长线上一点，动点P从点A出发沿AC方向以lcm/s的速度运动，同时动点Q从点C出发以相同的速度沿CA方向运动，当两点相遇时停止运动，过点P作AB的垂线，分别交⊙O于点M和点N，已知⊙O的半径为l，设运动时间为t秒．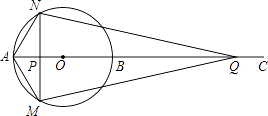
    （1）若AC=5，则当t=时，四边形AMQN为菱形；当t=时，NQ与⊙O相切；
    （2）当AC的长为多少时，存在t的值，使四边形AMQN为正方形？请说明理由，并求出此时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

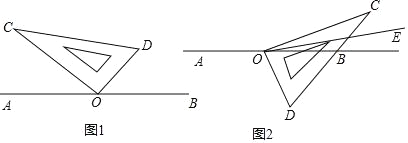
    【题目】如图，点O是直线AB上的一点，将一直角三角板如图摆放，过点O作射线OE平分∠BOC．

    （1）如图1，如果∠AOC=40°，依题意补全图形，写出求∠DOE度数的思路（不必写出完整的推理过程）；

    （2）当直角三角板绕点O顺时针旋转一定的角度得到图2，使得直角边OC在直线AB的上方，若∠AOC=α，其他条件不变，请你直接用含α的代数式表示∠DOE的度数；

    （3）当直角三角板绕点O继续顺时针旋转一周，回到图1的位置，在旋转过程中你发现∠AOC与∠DOE（0°≤∠AOC≤180°，0°≤∠DOE≤180°）之间有怎样的数量关系？请直接写出你的发现．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+c与x轴的一个交点为A（3，0），与y轴的交点为B（0，3），其顶点为C，对称轴为x=1．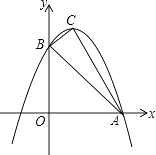

    （1）求抛物线的解析式；
    （2）已知点M为y轴上的一个动点，当△ABM为等腰三角形时，求点M的坐标；
    （3）将△AOB沿x轴向右平移m个单位长度（0＜m＜3）得到另一个三角形，将所得的三角形与△ABC重叠部分的面积记为S，用m的代数式表示S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在□ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．

    （1）求证：四边形EHFG是平行四边形；

    （2）□ABCD应满足什么条件时，四边形EHFG是矩形？并说明理由；

    （3）□ABCD应满足什么条件时，四边形EHFG是正方形？（不要说明理由）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图甲，在△ABC中，∠ACB=90°，AC=4cm，BC=3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：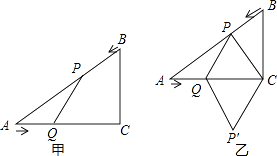

    （1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？
    （2）如图乙，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；′
    （3）当t为何值时，△APQ是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

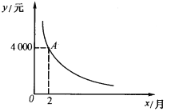
    【题目】李先生参加了某电脑公司推出的分期付款购买电脑活动，他购买的电脑价格为1.2万元，交了首付4000元之后每期付款y元，x个月结清余款．

    (1)写出y与x的函数关系式．

    (2)如打算每月付款不超过500元，李先生至少几个月才能结清余款？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是（A，B）的妙点．

    例如，如图1，点A表示的数为﹣1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的妙点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是（A，B）的妙点，但点D是（B，A）的妙点．

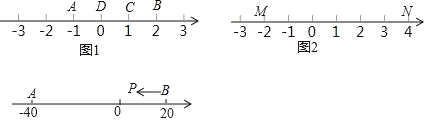
    知识运用：如图2，M、N为数轴上两点，点M所表示的数为﹣2，点N所表示的数为4．

    （1）数　 　所表示的点是（M，N）的妙点；

    （2）如图3，A、B为数轴上两点，点A所表示的数为﹣40，点B所表示的数为20．现有一只电子蚂蚁P从点B出发向左运动，到达点A停止．P点运动多少个单位时，P、A和B中恰有一个点为其余两点的妙点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】人民网为了解百姓对时事政治关心程度，特对18～35岁的青年人每天发微博数量进行调查，设一个人的“日均发微博条数”为m，规定：当m≥10时为甲级，当5≤m＜10时为乙级，当0≤m＜5时为丙级，现随机抽取20个符合年龄条件的青年人开展调查，所抽青年人的“日均发微博条数”的数据如下：

    0

    8

    2

    8

    10

    13

    7

    5

    7

    3

    12

    10

    7

    11

    3

    6

    8

    14

    15

    12


    （1）样本数据中为甲级的频率为；（直接填空）
    （2）求样本中乙级数据的中位数和众数．
    （3）从样本数据为丙级的人中随机抽取2人，用列举法或树状图求抽得2个人的“日均发微博条数”都是3的概率．

    查看答案和解析>>

    同步练习册答案