
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.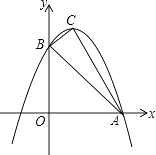
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
【答案】
(1)
解:由题意可知,抛物线y=ax2+bx+c与x轴的另一个交点为(﹣1,0),则
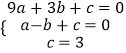 ,
,
解得 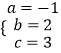 .
.
故抛物线的解析式为y=﹣x2+2x+3
(2)
解:依题意:设M点坐标为(0,t),
①当MA=MB时:
![]()
解得t=0,
故M(0,0);
②当AB=AM时:
![]()
解得t=3(舍去)或t=﹣3,
故M(0,﹣3);
③当AB=BM时,
![]()
解得t=3±3 ![]() ,
,
故M(0,3+3 ![]() )或M(0,3﹣3
)或M(0,3﹣3 ![]() ).
).
所以点M的坐标为:(0,0)、(0,﹣3)、(0,3+3 ![]() )、(0,3﹣3
)、(0,3﹣3 ![]() )
)
(3)
解:平移后的三角形记为△PEF.
设直线AB的解析式为y=kx+b,则
![]() ,
,
解得 ![]() .
.
则直线AB的解析式为y=﹣x+3.
△AOB沿x轴向右平移m个单位长度(0<m<3)得到△PEF,
易得直线EF的解析式为y=﹣x+3+m.
设直线AC的解析式为y=k′x+b′,则
![]() ,
,
解得 ![]() .
.
则直线AC的解析式为y=﹣2x+6.
连结BE,直线BE交AC于G,则G( ![]() ,3).
,3).
在△AOB沿x轴向右平移的过程中.
①当0<m≤ ![]() 时,如图1所示.
时,如图1所示.
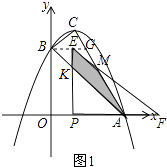
设PE交AB于K,EF交AC于M.
则BE=EK=m,PK=PA=3﹣m,
联立 ![]() ,
,
解得 ![]() ,
,
即点M(3﹣m,2m).
故S=S△PEF﹣S△PAK﹣S△AFM
= ![]() PE2﹣
PE2﹣ ![]() PK2﹣
PK2﹣ ![]() AFh
AFh
= ![]() ﹣
﹣ ![]() (3﹣m)2﹣
(3﹣m)2﹣ ![]() m2m
m2m
=﹣ ![]() m2+3m.
m2+3m.
②当 ![]() <m<3时,如图2所示.
<m<3时,如图2所示.
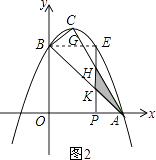
设PE交AB于K,交AC于H.
因为BE=m,所以PK=PA=3﹣m,
又因为直线AC的解析式为y=﹣2x+6,
所以当x=m时,得y=6﹣2m,
所以点H(m,6﹣2m).
故S=S△PAH﹣S△PAK
= ![]() PAPH﹣
PAPH﹣ ![]() PA2
PA2
=﹣ ![]() (3﹣m)(6﹣2m)﹣
(3﹣m)(6﹣2m)﹣ ![]() (3﹣m)2
(3﹣m)2
= ![]() m2﹣3m+
m2﹣3m+ ![]() .
.
综上所述,当0<m≤ ![]() 时,S=﹣
时,S=﹣ ![]() m2+3m;当
m2+3m;当 ![]() <m<3时,S=
<m<3时,S= ![]() m2﹣3m+
m2﹣3m+ ![]() .
.
【解析】(1)根据对称轴可知,抛物线y=ax2+bx+c与x轴的另一个交点为(﹣1,0),根据待定系数法可得抛物线的解析式为y=﹣x2+2x+3.(2)分三种情况:①当MA=MB时;②当AB=AM时;③当AB=BM时;三种情况讨论可得点M的坐标.(3)平移后的三角形记为△PEF.根据待定系数法可得直线AB的解析式为y=﹣x+3.易得AB平移m个单位所得直线EF的解析式为y=﹣x+3+m.根据待定系数法可得直线AC的解析式.连结BE,直线BE交AC于G,则G( ![]() ,3).在△AOB沿x轴向右平移的过程中.根据图象,易知重叠部分面积有两种情况:①当0<m≤
,3).在△AOB沿x轴向右平移的过程中.根据图象,易知重叠部分面积有两种情况:①当0<m≤ ![]() 时;②当
时;②当 ![]() <m<3时;讨论可得用m的代数式表示S.
<m<3时;讨论可得用m的代数式表示S.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是 . 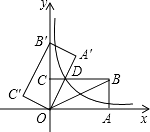
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() 的下列说法正确的是( )
的下列说法正确的是( )
① 该函数的图象在第二、四象限;
② A(x1、y1)、B(x2、y2)两点在该函数图象上,若x1<x2,则y1<y2;
③ 当x>2时,则y>-2;
④ 若反比例函数y=![]() 与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
A. ① ③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校2400名学生的阅读兴趣,从中随机抽查了部分同学,就“我最感兴趣的书籍”进行了调查:A.小说、B.散文、C.科普、D.其他(每个同学只能选择一项),进行了相关统计,整理并绘制出两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
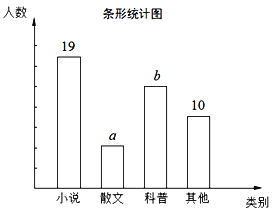

(1)本次抽查中,样本容量为______;
(2)a=______,b=______;
(3)扇形统计图中,其他类书籍所在扇形的圆心角是______°;
(4)请根据样本数据,估计全校有多少名学生对散文感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张家界市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图像交于A(2,4),B(-4,n)两点,交x轴于点C.
的图像交于A(2,4),B(-4,n)两点,交x轴于点C.

(1)求m、n的值;
(2)请直接写出不等式kx+b<![]() 的解集;
的解集;
(3)将x轴下方的图像沿x轴翻折,点B落在点B′处,连接AB′、B′C,求△A B′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a![]() b是新规定的一种运算法则:a
b是新规定的一种运算法则:a![]() b=a2+ab,例如3
b=a2+ab,例如3![]() (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)![]() 5的值;
5的值;
(2)若(﹣2)![]() x=6,求x的值;
x=6,求x的值;
(3)若3![]() (2
(2![]() x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com