
【题目】人民网为了解百姓对时事政治关心程度,特对18~35岁的青年人每天发微博数量进行调查,设一个人的“日均发微博条数”为m,规定:当m≥10时为甲级,当5≤m<10时为乙级,当0≤m<5时为丙级,现随机抽取20个符合年龄条件的青年人开展调查,所抽青年人的“日均发微博条数”的数据如下:
0 | 8 | 2 | 8 | 10 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)样本数据中为甲级的频率为;(直接填空)
(2)求样本中乙级数据的中位数和众数.
(3)从样本数据为丙级的人中随机抽取2人,用列举法或树状图求抽得2个人的“日均发微博条数”都是3的概率.
【答案】
(1)0.4
(2)
解:数据中5≤m<10的为8,8,7,5,7,7,6,8,
按照从小到大顺序排列为5,6,7,7,7,8,8,8,
则中位数是7,众数是7或8
(3)
解:数据中0≤m<5的为0,2,3,3,
列表如下:
0 | 2 | 3 | 3 | |
0 | ﹣﹣﹣ | (2,0) | (3,0) | (3,0) |
2 | (0,2) | ﹣﹣﹣ | (3,2) | (3,2) |
3 | (0,3) | (2,3) | ﹣﹣﹣ | (3,3) |
3 | (0,3) | (2,3) | (3,3) | ﹣﹣﹣ |
所有等可能的情况有12种,其中抽得2个人的“日均发微博条数”都是3的有2种,
P(抽得2人的“日均发微博条数”都是3)= ![]() =
= ![]()
【解析】解:(1)数据中m≥10的为10,13,12,10,11,14,15,12共8个,
则样本数据中为甲级的频率为 ![]() =0.4;
=0.4;
故答案为:0.4;
(1)找出m≥10的个数,除以20即可得到结果;(2)找出5≤m<10的个数,确定出中位数与众数即可;(3)找出0≤m<5的个数,列表得出所有等可能的情况数,即可求出所求的概率.


科目:初中数学 来源: 题型:
【题目】张家界市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a![]() b是新规定的一种运算法则:a
b是新规定的一种运算法则:a![]() b=a2+ab,例如3
b=a2+ab,例如3![]() (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)![]() 5的值;
5的值;
(2)若(﹣2)![]() x=6,求x的值;
x=6,求x的值;
(3)若3![]() (2
(2![]() x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题.
(1)商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商品制定了两种优惠方法:
①买一只茶壶赠一只茶杯;②按总价的90%付款.某顾客购买茶壶5只,茶杯若干只(不少于5只),问顾客买多少只茶杯时,两种方法付款相同.假如该顾客买了茶杯20只,哪种买法实惠?
(2)某人原计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达,但他因事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A,B两地间的距离.
(3)某工厂完成一批产品,一车间单独完成需30天,二车间单独完成需20天.
①如一车间先做若干天,然后由二车间继续做,直至完成,前后共做了25天,问一车间先做了几天?
②如一车间先做了3天后,二车间加入一起做,还需多少天才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在线段EF上,点M、N分别是线段EA、BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
![]()
A. 10 cm B. 11 cm C. 12 cm D. 13 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为直线AB上一点,将一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板的一边ON与射线OB重合,过点O在三角板的内部,作射线OC,使∠NOC:∠MOC=2:1,求∠AOC的度数;
(2)如图2,将三角板绕点O逆时针旋转一定角度到图2的位置,过点O在三角板MON的内部作射线OC,使得OC恰好是∠MOB对的角平分线,此时∠AOM与∠NOC满足怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
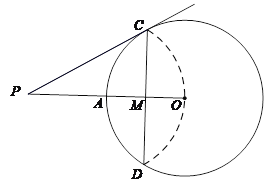
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com