
【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
![]()
【答案】(1)-4;(2)0;(3)符合条件的t的值是0.5,2或8.
【解析】试题(1)根据数轴写出即可;(2)先根据路程=速度×时间求出B点2秒运动的路程,再加上-4即可求解;(3)分三种情况:①O为BA的中点;②B为OA的中点;③当点A是线段OB的中点时;进行讨论即可求解.
(1)点B表示的数是___-4__;
(2)2秒后点B表示的数是 0 ;
(3)① 当点O是线段AB的中点时,OB=OA
4-3t=2+t
t=0.5
② 当点B是线段OA的中点时, OA = 2 OB
2+t=2(3t-4)
t=2
③ 当点A是线段OB的中点时, OB = 2 OA
3t--4=2(2+t)
t=8
综上所述,符合条件的t的值是0.5,2或8.


科目:初中数学 来源: 题型:
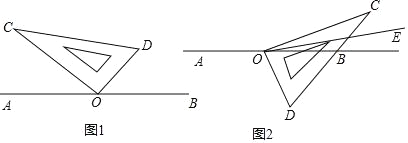
【题目】如图,点O是直线AB上的一点,将一直角三角板如图摆放,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=40°,依题意补全图形,写出求∠DOE度数的思路(不必写出完整的推理过程);
(2)当直角三角板绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,请你直接用含α的代数式表示∠DOE的度数;
(3)当直角三角板绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
查看答案和解析>>
科目:初中数学 来源: 题型:
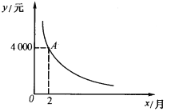
【题目】李先生参加了某电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为1.2万元,交了首付4000元之后每期付款y元,x个月结清余款.
(1)写出y与x的函数关系式.
(2)如打算每月付款不超过500元,李先生至少几个月才能结清余款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的妙点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的妙点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的妙点,但点D是(B,A)的妙点.
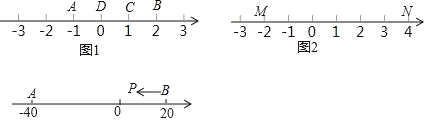
知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
(1)数 所表示的点是(M,N)的妙点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发向左运动,到达点A停止.P点运动多少个单位时,P、A和B中恰有一个点为其余两点的妙点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.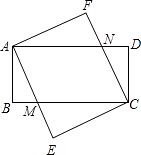
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第6个小房子用的石子数量为 ( )

A. 87 B. 77 C. 70 D. 60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民网为了解百姓对时事政治关心程度,特对18~35岁的青年人每天发微博数量进行调查,设一个人的“日均发微博条数”为m,规定:当m≥10时为甲级,当5≤m<10时为乙级,当0≤m<5时为丙级,现随机抽取20个符合年龄条件的青年人开展调查,所抽青年人的“日均发微博条数”的数据如下:
0 | 8 | 2 | 8 | 10 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)样本数据中为甲级的频率为;(直接填空)
(2)求样本中乙级数据的中位数和众数.
(3)从样本数据为丙级的人中随机抽取2人,用列举法或树状图求抽得2个人的“日均发微博条数”都是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在y轴的正半轴上,点A在x轴的正半轴上,点C的坐标为(0,8),将△ABC沿直线AB折叠,点C落在x轴的负半轴D(﹣4,0)处.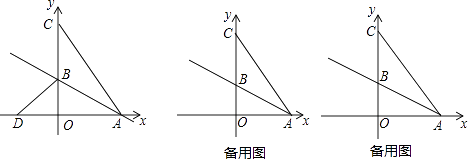
(1)求直线AB的解析式;
(2)点P从点A出发以每秒4 ![]() 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);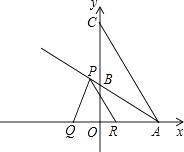
(3)在(2)的条件下,点N是射线AB上一点,以点N为圆心,同时经过R、Q两点作⊙N,⊙N交y轴于点E,F.是否存在t,使得EF=RQ?若存在,求出t的值,并求出圆心N的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com