
【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.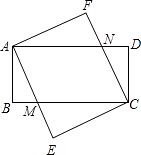
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB=CD,AD∥BC,
∵四边形AECF是矩形,∴AE∥CF,
∴四边形AMCN是平行四边形,
∴AM=CN,
在Rt△ABM和Rt△CDN中,
∵ ![]() ,
,
∴Rt△ABM≌Rt△CDN(HL)
(2)
解:当AB=AF时,四边形AMCN是菱形,
理由:∵四边形ABCD、AECF是矩形,
∴∠B=∠BAD=∠EAF=∠F=90°,
∴∠BAD﹣∠NAM=∠EAF﹣∠NAM,即∠BAM=∠FAN,
在△ABM和△AFN中∠BAM=∠FAN,AB=AF,∠B=∠F
∵ 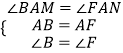 ,
,
∴△ABM≌△AFN(ASA),
∴AM=AN,
由(1)知四边形AMCN是平行四边形,
∴平行四边形AMCN是菱形.
【解析】(1)利用矩形的性质结合平行四边形的判定于性质得出AM=CN,进而得出Rt△ABM≌Rt△CDN;(2)利用全等三角形的判定得出△ABM≌△AFN(ASA),进而得出四边形AMCN是菱形.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() 的下列说法正确的是( )
的下列说法正确的是( )
① 该函数的图象在第二、四象限;
② A(x1、y1)、B(x2、y2)两点在该函数图象上,若x1<x2,则y1<y2;
③ 当x>2时,则y>-2;
④ 若反比例函数y=![]() 与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
A. ① ③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图像交于A(2,4),B(-4,n)两点,交x轴于点C.
的图像交于A(2,4),B(-4,n)两点,交x轴于点C.

(1)求m、n的值;
(2)请直接写出不等式kx+b<![]() 的解集;
的解集;
(3)将x轴下方的图像沿x轴翻折,点B落在点B′处,连接AB′、B′C,求△A B′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程x2-(2k+1)x+4k-2=0
的方程x2-(2k+1)x+4k-2=0
(1)求证:不论k取何值,这个方程总有实数根
(2)若等腰△ABC一边长a=4,另两边长b,c恰好是这个方程的两根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABM=37°,AB=20,C是射线BM上一点.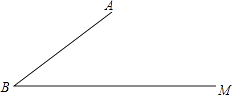
(1)求点A到BM的距离;
(2)在下列条件中,可以唯一确定BC长的是;(填写所有符合条件的序号)
①AC=13;②tan∠ACB= ![]() ;③连接AC,△ABC的面积为126.
;③连接AC,△ABC的面积为126.
(3)在(2)的答案中,选择一个作为条件,画出草图,求BC.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a![]() b是新规定的一种运算法则:a
b是新规定的一种运算法则:a![]() b=a2+ab,例如3
b=a2+ab,例如3![]() (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)![]() 5的值;
5的值;
(2)若(﹣2)![]() x=6,求x的值;
x=6,求x的值;
(3)若3![]() (2
(2![]() x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在线段EF上,点M、N分别是线段EA、BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
![]()
A. 10 cm B. 11 cm C. 12 cm D. 13 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)写出数轴上A、B两点表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,t为何值时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com