
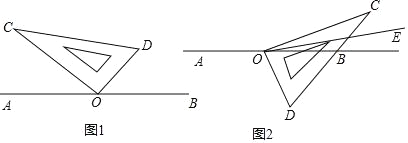
【题目】如图,点O是直线AB上的一点,将一直角三角板如图摆放,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=40°,依题意补全图形,写出求∠DOE度数的思路(不必写出完整的推理过程);
(2)当直角三角板绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,请你直接用含α的代数式表示∠DOE的度数;
(3)当直角三角板绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
【答案】(1)见解析;(2)∠DOE=![]() ;(3)∠DOE=
;(3)∠DOE=![]() ∠AOC(0°≤∠AOC≤180°),∠DOE=180°
∠AOC(0°≤∠AOC≤180°),∠DOE=180°![]() ∠AOC(0°≤∠DOE≤180°).
∠AOC(0°≤∠DOE≤180°).
【解析】
(1) 根据角平分线的作法作出OE平分∠BOC,先根据平角的定义求出∠BOC, 再根据角平分线的定义求出∠COE, 再根据直角的定义即可求解;
(2) 先根据平角的定义求出∠BOC, 再根据角平分线的定义求出∠COE, 再根据直角的定义即可求解;
(3) 分两种情况: ![]() ≤∠AOC≤
≤∠AOC≤![]() ,
, ![]() ≤∠DOE≤
≤∠DOE≤![]() , 可求∠AOC与∠DOE之间的数量关系.
, 可求∠AOC与∠DOE之间的数量关系.
解:(1)如图1,补全图形;
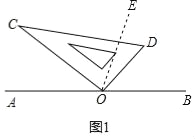
解题思路如下:
①由∠AOC+∠BOC=180°,∠AOC=40°,
得∠BOC=140°;
②由OE平分∠BOC,
得∠COE=70°;
③由直角三角板,
得∠COD=90°;
④由∠COD=90°,∠COE=70°,
得∠DOE=20°.
(2)①由∠AOC+∠BOC=180°,∠AOC=α,
得∠BOC=180°﹣α;
②由OE平分∠BOC,
得∠COE=90°﹣![]() α;
α;
③由直角三角板,
得∠COD=90°;
④由∠COD=90°,∠COE=90°﹣![]() α,
α,
得∠DOE=![]() .
.
(3)∠DOE=![]() ∠AOC(0°≤∠AOC≤180°),∠DOE=180°
∠AOC(0°≤∠AOC≤180°),∠DOE=180°![]() ∠AOC(0°≤∠DOE≤180°).
∠AOC(0°≤∠DOE≤180°).


科目:初中数学 来源: 题型:
【题目】阅读下面材料: 小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:求∠ACE的度数,AC的长.
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.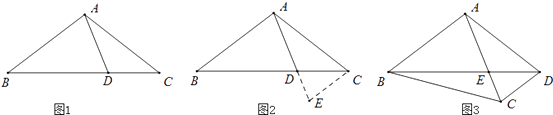
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() 的下列说法正确的是( )
的下列说法正确的是( )
① 该函数的图象在第二、四象限;
② A(x1、y1)、B(x2、y2)两点在该函数图象上,若x1<x2,则y1<y2;
③ 当x>2时,则y>-2;
④ 若反比例函数y=![]() 与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
A. ① ③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校2400名学生的阅读兴趣,从中随机抽查了部分同学,就“我最感兴趣的书籍”进行了调查:A.小说、B.散文、C.科普、D.其他(每个同学只能选择一项),进行了相关统计,整理并绘制出两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
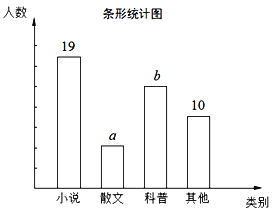

(1)本次抽查中,样本容量为______;
(2)a=______,b=______;
(3)扇形统计图中,其他类书籍所在扇形的圆心角是______°;
(4)请根据样本数据,估计全校有多少名学生对散文感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张家界市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com