
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB. 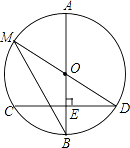
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
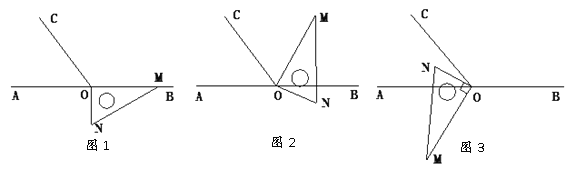
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
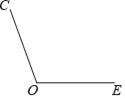
【题目】已知∠EOC=110°,将角的一边OE绕点O旋转,使终止位置OD和起始位置OE成一条直线,以点O为中心将OC顺时针旋转到OA,使∠COA=∠DOC,过点O作∠COA的平分线OB.
(1)借助量角器、直尺补全图形;
(2)求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春运期间,宁波火车站加大了安检力度,原来在北广场执勤的有10人,在南广场执勤的有6人,现调50人去支援.设调往北广场x人.
(1)则南广场增援后有执勤多少人(用含x的代数式表示).
(2)若要使在北广场执勤人数是在南广场执勤人数的2倍,问应调往北广场、南广场两处各多少人?
(3)通过适当的调配支援人数,使在北广场执勤人数恰好是在南广场执勤人数的n倍(n是大于1的正整数,不包括1).求符合条件的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
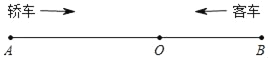
【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com