
����Ŀ���ڴ����ڼ䣬������վ�Ӵ��˰������ȣ�ԭ���ڱ��㳡ִ�ڵ���10�ˣ����Ϲ㳡ִ�ڵ���6�ˣ��ֵ�50��ȥ֧Ԯ����������㳡x�ˣ�
��1�����Ϲ㳡��Ԯ����ִ�ڶ����ˣ��ú�x�Ĵ���ʽ��ʾ����
��2����Ҫʹ�ڱ��㳡ִ�����������Ϲ㳡ִ��������2������Ӧ�������㳡���Ϲ㳡�����������ˣ�
��3��ͨ���ʵ��ĵ���֧Ԯ������ʹ�ڱ��㳡ִ������ǡ�������Ϲ㳡ִ��������n����n�Ǵ���1����������������1���������������n��ֵ��
���𰸡���1��56��x�ˣ���2���������㳡34�ˣ�������Ϲ㳡16������3��2��5��10��
��������
��1����������㳡x�ˣ�������Ϲ㳡��50��x���ˣ�
��2����������㳡x�ˣ�������Ϲ㳡��50��x���ˣ�������õ�����ϵ���ڱ��㳡ִ������=���Ϲ㳡ִ��������2�����ݵ�����ϵ�г����̣��ٽ⼴�ɣ�
��3����������㳡x�ˣ�������Ϲ㳡��50��x���ˣ�������õ�����ϵ���ڱ��㳡ִ������=���Ϲ㳡ִ��������n�����ݵ�����ϵ�г����̣�����������⼴�ɣ�
��1����������㳡x�ˣ�������Ϲ㳡��50��x���ˣ�
���Ϲ㳡��Ԯ����ִ��50��x+6=56��x
�ʴ�Ϊ��56��x��
��2����������㳡x�ˣ�������Ϲ㳡��50��x���ˣ�������ã�
10+x=2��6+50��x����
��ã�x=34
�����Ϲ㳡������50��34=16���ˣ���
�ʵ������㳡34�ˣ�������Ϲ㳡16�ˣ�
��3����������㳡x�ˣ�������Ϲ㳡��50��x���ˣ�������ã�
10+x=n��6+50��x����
10+x=n��56��x����
![]()
��ã�![]()
![]()
![]()
�ʴ�Ϊ��2��5��10��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н������Ϣ������ҵ���ԣ�����ѧ����ǩ�ķ�ʽ�����Լ��Ŀ������ݣ��涨��ÿλ�����������������⣨��ǩ�ֱ��ô���B1��B2��B3��ʾ���г�ȡһ�������������ϻ��⣨��ǩ�ֱ��ô���J1��J2��J3��ʾ���г�ȡһ�����п��ԣ�С���ڿ�������ǩ������£��ֱ�ӱ�������ϻ���������س�ȡһ����ǩ��
��1������״ͼ���б�����ʾ�����п��ܵĽ����
��2����С���鵽�ı�������ϻ������ǩ������±꣨���硰B1�����±�Ϊ��1����Ϊһ������һ��ż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
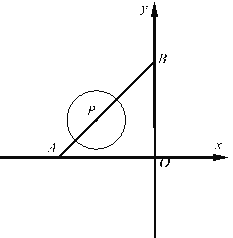
����Ŀ����ͼ1��ֱ��![]() �ֱ�x�ᡢy����A��B���㣬��P���߶�AB�ϵ�һ���㣬��PΪԲ�ģ�rΪ�뾶��Բ��
�ֱ�x�ᡢy����A��B���㣬��P���߶�AB�ϵ�һ���㣬��PΪԲ�ģ�rΪ�뾶��Բ��
��1������P�ĺ�����Ϊ��3������P��x������ʱ����뾶rΪ ����ʱ��P��y���λ�ù�ϵ�� .��ֱ��д�����
��2����![]() ������P������������ֻ��3��������ʱ�����P������.
������P������������ֻ��3��������ʱ�����P������.
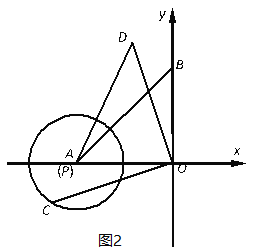
��3����ͼ2����Բ��P��A�غϣ�![]() ʱ�����CΪ��P�ϵ�һ�����㣬����OC�����߶�OC�Ƶ�O˳ʱ����ת90�����õ��߶�OD������AD����AD������ֵ��ֱ��д����Ӧ�ĵ�D�����꣮
ʱ�����CΪ��P�ϵ�һ�����㣬����OC�����߶�OC�Ƶ�O˳ʱ����ת90�����õ��߶�OD������AD����AD������ֵ��ֱ��д����Ӧ�ĵ�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CD=24����M�ڡ�O�ϣ�MD����Բ��O������MB�� 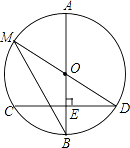
��1����BE=8�����O�İ뾶��
��2������DMB=��D�����߶�OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ10����B�ڵ�A��ߣ���AB=18������P�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��1��д�������ϵ�B��ʾ��������P��ʾ�������ú�t�Ĵ���ʽ��ʾ����
��2������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ������
���ʵ�P�˶�������ʱ�ϵ�Q��
���ʵ�P�˶�������ʱ���Q���4����λ���ȣ��������ʱ��P��ʾ������
��3������P��Q�ԣ�2���е��ٶ�ͬʱ�ֱ�ӵ�A��B�����˶���ͬʱ��R��ԭ��O��ÿ��7����λ���ٶ������˶����Ƿ���ڳ���m��ʹ��2QR+3OP��mORΪ��ֵ�������������mֵ�Լ������ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��̣�
(1)2(10��0.5y)����(1.5y+2)
(2)![]() (x��5)��3��
(x��5)��3��![]() (x��5)
(x��5)
(3)![]() ��1��
��1��![]()
(4)x��![]() (x��9)��
(x��9)��![]() [x+
[x+![]() (x��9)]
(x��9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ24���ף��ס���������ͬʱ�Ӷ���A����������2����/����ٶ��������εı߰�˳ʱ�뷽���ƶ�������4����/����ٶ��������εı߰���ʱ�뷽���ƶ���ÿ����������ҵ��ٶȾ�����1����/���Ҷ��ı�ԭ�����ƶ�������Ĵ�����ʱ�����������ľ�����______���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD�������������µ���������AB��40�ף�AB���е�ΪP������B���Ĵ�ֱ�߶�Ϊ6�ף��罭������������Ȼ�´����Ƴ��������Σ�Ϊ�˱�֤������ֻ�İ�ȫ�������´�����͵���ĸ߶Ȳ�������30�ף���֪�����ھ�����B����50�ĵ���E��ǡ�ÿ�����E��P��C��һֱ���ϣ�������ǰ��150��ӵ���F��ǡ�ÿ�����F��A��C��һֱ���ϣ�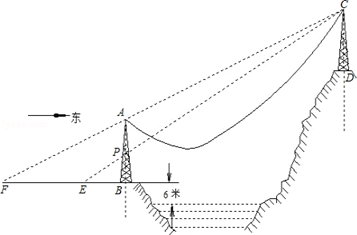
��1��������������ľ��루��ֱ��AB��CD��ľ��룩��
��2�����Ե�AΪ����ԭ�㣬��ˮƽ����Ϊx�ᣬȡ��λ����Ϊ1�ף�BA���ӳ�����Ϊy�Ὠ������ϵ����պ�������߶�Ҫ�����������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M���߶�AB�е㣬AD��BC���ڵ�N������AC��BD��MC��MD����l=��2����3=��4��
��1����֤����AMD�ա�BMC��
��2��ͼ���ڲ������µ���ĸ������£���д����������AMD�ա�BMC�����������ȫ�������Σ���ѡ������һ�Խ���֤����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com