
【题目】如图,已知数轴上点A表示的数为10,点B在点A左边,且AB=18.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.
①问点P运动多少秒时追上点Q?
②问点P运动多少秒时与点Q相距4个单位长度?并求出此时点P表示的数;
(3)若点P、Q以(2)中的速度同时分别从点A、B向右运动,同时点R从原点O以每秒7个单位的速度向右运动,是否存在常数m,使得2QR+3OP﹣mOR为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.

【答案】(1)﹣8; 10﹣5t;(2)①9秒;②7秒或11秒;-25或-45;(3)![]() .
.
【解析】
(1)根据两点间的距离公式,以及路程=速度![]() 时间即可求解;
时间即可求解;
(2)①根据时间=路程差![]() 速度差,列出算式计算即可求解;
速度差,列出算式计算即可求解;
②分两种情况:相遇前相距4个单位长度;相遇后相距4个单位长度;进行讨论可求点P表示的数;
(3) 设t秒后2QR+3OP﹣mOR为定值,列方程求解即可.
解:(1)数轴上点B表示的数为10﹣18=﹣8,点P表示的数为10﹣5t;
(2)①18÷(5﹣3)=9(秒).
故点P运动9秒时追上点Q;
②相遇前相距4个单位长度,
(18﹣4)÷(5﹣3)=7(秒),
10﹣7×5=﹣25,
则点P表示的数为﹣25;
相遇后相距4个单位长度,
(18+4)÷(5﹣3)=11(秒),
10﹣11×5=﹣45,
则点P表示的数为﹣45;
(3)设t秒后2QR+3OP﹣mOR为定值,
由题意得,2QR+3OP﹣mOR=2×[7t﹣(3t﹣8)]+3(10+5t)﹣7mt=(23﹣7m)t+46,
∴当m=![]() 时,2QR+3OP﹣mOR为定值46.
时,2QR+3OP﹣mOR为定值46.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长的数值与面积的数值相等,则点P是和谐点.
(1)判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=﹣x+b(b为常数)上,求a,b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
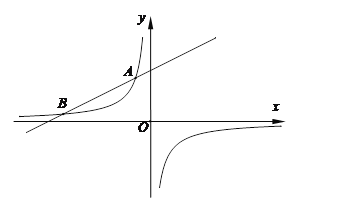
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(-2,6)、点B(
的图象交于点A(-2,6)、点B(![]() ,1).
,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
(3)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移n个单位,使平移后的图象与反比例函数
轴向下平移n个单位,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求n的值.
的图象有且只有一个交点,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
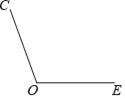
【题目】已知∠EOC=110°,将角的一边OE绕点O旋转,使终止位置OD和起始位置OE成一条直线,以点O为中心将OC顺时针旋转到OA,使∠COA=∠DOC,过点O作∠COA的平分线OB.
(1)借助量角器、直尺补全图形;
(2)求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
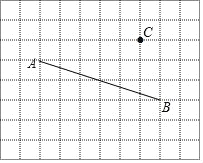
【题目】利用网格画图:
(1)过点C画AB的平行线;
(2)过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中, 线段最短,理由: ;
(4)点C到直线AB的距离是线段的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春运期间,宁波火车站加大了安检力度,原来在北广场执勤的有10人,在南广场执勤的有6人,现调50人去支援.设调往北广场x人.
(1)则南广场增援后有执勤多少人(用含x的代数式表示).
(2)若要使在北广场执勤人数是在南广场执勤人数的2倍,问应调往北广场、南广场两处各多少人?
(3)通过适当的调配支援人数,使在北广场执勤人数恰好是在南广场执勤人数的n倍(n是大于1的正整数,不包括1).求符合条件的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( ) 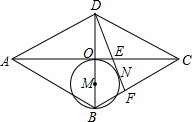
A.3
B.4
C.4.8
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
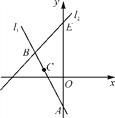
【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
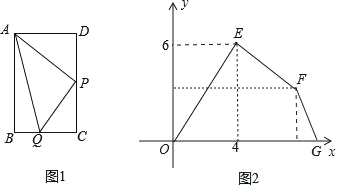
【题目】如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com