
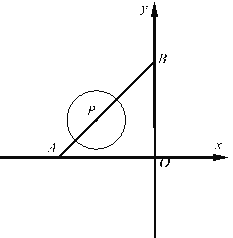
【题目】如图1,直线![]() 分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
(1)若点P的横坐标为﹣3,当⊙P与x轴相切时,则半径r为 ,此时⊙P与y轴的位置关系是 .(直接写结果)
(2)若![]() ,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
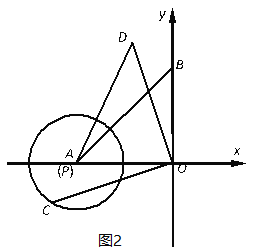
(3)如图2,当圆心P与A重合,![]() 时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
【答案】(1)![]() ,相离,(2)P
,相离,(2)P![]() 或P
或P![]() ;(3)当点D在线段AB上时,AD最小值为
;(3)当点D在线段AB上时,AD最小值为![]() ,点D坐标为
,点D坐标为![]() ,当点D在线段AB的延长线上时,AD最大值为
,当点D在线段AB的延长线上时,AD最大值为![]() ,点D坐标为
,点D坐标为![]()
【解析】
(1)根据坐标轴上点的坐标特征求出A点和B点的坐标,根据相似三角形的性质解答;
(2)根据直线与圆的位置关系解答;
(3)连接AC,BD,证明△AOC≌△BOD,求出BD的长,得到AD最长或最短距离,根据直角三角形的性质求出点D的坐标.
(1)当x=0时,y=4, 当y=0时,x=-4,
∴A点的坐标为(-4,0),B点的坐标为(0,4),
点N为⊙P与x轴的切点,连接PN,
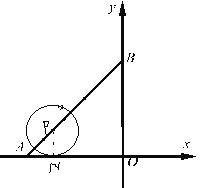
则PN∥OB,
∴![]() ,即
,即![]() ,
,
解得,PN=1,
x+4=1,
解得,x=3,
∵3>1,
∴⊙P与y轴的位置关系是相离,
故答案为:1;相离;
(2)当r=![]() ,⊙P与x轴相切时,
,⊙P与x轴相切时,
由![]() =x+4,得x=
=x+4,得x=![]() ,
,
则⊙P与y轴相交,
此时点P的坐标为(![]() ,
,![]() ),
),
当r=![]() ,⊙P与y轴相切时,
,⊙P与y轴相切时,
由y=![]() +4=
+4=![]() ,
,
则P与x轴相交,
此时点P的坐标为(-![]() ,
,![]() );
);
(3)连接AC、BD,
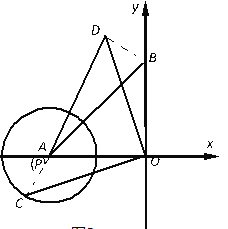
∵∠COD=∠AOB=90°
∴∠COA=∠DOB
易证△AOC≌△BOD
∴BD=AC=2
∴点D的运动轨迹是以点B为圆心,2为半径的圆,
当点D在线段AB上时,AD最小值为![]() ,点D坐标为
,点D坐标为![]() ;
;
当点D在线段AB的延长线上时,AD最大值为![]() ,点D坐标为
,点D坐标为![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】某校允许学生在同个系列的校服里选择不同款式,新生入学后,学校就新生对校服款式选择情况作了抽样调查,调查分为款式A、B、C、D四种,每位新生只能选择一种款式,现将调查统计结果制成了如下两幅不完整的统计图,请结合这两幅统计图,回答下列问题:
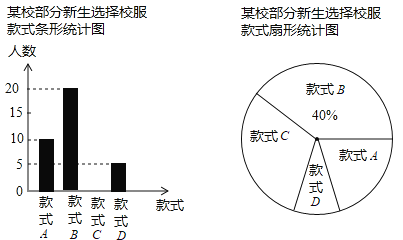
(1)在本次调查中,一共抽取了多少名新生,并补全条形统计图;
(2)若该校有847名新生,服装厂已生产了270套B款式的校服,请你按相关统计知识判断是否还要继续生产B款式的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
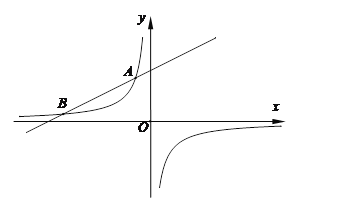
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(-2,6)、点B(
的图象交于点A(-2,6)、点B(![]() ,1).
,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
(3)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移n个单位,使平移后的图象与反比例函数
轴向下平移n个单位,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求n的值.
的图象有且只有一个交点,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
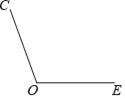
【题目】已知∠EOC=110°,将角的一边OE绕点O旋转,使终止位置OD和起始位置OE成一条直线,以点O为中心将OC顺时针旋转到OA,使∠COA=∠DOC,过点O作∠COA的平分线OB.
(1)借助量角器、直尺补全图形;
(2)求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春运期间,宁波火车站加大了安检力度,原来在北广场执勤的有10人,在南广场执勤的有6人,现调50人去支援.设调往北广场x人.
(1)则南广场增援后有执勤多少人(用含x的代数式表示).
(2)若要使在北广场执勤人数是在南广场执勤人数的2倍,问应调往北广场、南广场两处各多少人?
(3)通过适当的调配支援人数,使在北广场执勤人数恰好是在南广场执勤人数的n倍(n是大于1的正整数,不包括1).求符合条件的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y= ![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= ![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒 ![]() 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com