
����Ŀ����ͼ��1������ƽ��ֱ������ϵ�У�����ABCO��B������Ϊ��4��3����������y= ![]() x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬ֱ��AD��y�ύ��E�㣬��������y=
x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬ֱ��AD��y�ύ��E�㣬��������y= ![]() x2+bx+c���ڵ�������F�㣮
x2+bx+c���ڵ�������F�㣮
��1����������߽���ʽ��F�����ꣻ
��2����ͼ��2��������P�ӵ�C���������߶�CB��ÿ��1����λ���ȵ��ٶ����յ�B�˶���ͬʱ������M�ӵ�A���������߶�AE��ÿ�� ![]() ����λ���ȵ��ٶ����յ�E�˶�������P��PH��OA������ΪH������MP��MH�����P���˶�ʱ��Ϊt��
����λ���ȵ��ٶ����յ�E�˶�������P��PH��OA������ΪH������MP��MH�����P���˶�ʱ��Ϊt��
����EP+PH+HF�Ƿ�����Сֵ������У����t��ֵ�����û�У���˵�����ɣ�
������PMH�ǵ��������Σ���ֱ��д����ʱt��ֵ��
���𰸡�
��1��
�⣺�߾���ABCO��B������Ϊ��4��3��
��C��������0��3��
��������y= ![]() x2+bx+c��������ABCO�Ķ���B��C��
x2+bx+c��������ABCO�Ķ���B��C��
�� ![]() ��
��
��ã� ![]() ��
��
��������߽���ʽy=�� ![]() x2+2x+3��
x2+2x+3��
��ֱ��AD�Ľ���ʽΪy=k1x+b1
��A��4��0����D��2��3����
�� ![]() ��
��  ��
��
�� ![]() ��
��
���� 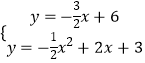 ��
��
��F���ڵ������ޣ�
��F��6����3����
��2��
�⣺�١�E��0��6������CE=CO������ͼ��1������

����CF��x����H�䣬��H����BC�Ĵ��߽�BC��P�䣬��P
�˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С��
��ֱ��CF�Ľ���ʽΪy=k2x+b2
��C��0��3����F��6����3����
�� ![]() ��
��
��ã� ![]() ��
��
��y=��x+3
��y=0ʱ��x=3��
��H�䣨3��0����
��CP=3����t=3��
����ͼ1��M��MN��OA��OA��N��
�ߡ�AMN�ס�AEO��
�� ![]() ��
��
�� ![]() ��
��
��AN=t��MN= ![]() ��
��
I��ͼ3����PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ�
��MN= ![]() PH��
PH��
��MN= ![]() ��
��
��t=1��
II��ͼ1����HM=HPʱ��MH=3��MN= ![]() ��
��
HN=OA��AN��OH=4��2t ��Rt��HMN��MN2+HN2=MH2��
�� ![]() ��
��
��25t2��64t+28=0��
��ã�t1=2����ȥ���� ![]() ��
��
III��ͼ2��ͼ4����PH=PMʱ��
��PM=3��MT= ![]() ��PT=BC��CP��BT=|4��2t|��
��PT=BC��CP��BT=|4��2t|��
����Rt��PMT��MT2+PT2=PM2��
�� ![]() ��
��
��25t2��100t+64=0��
��ã� ![]() ��
�� ![]()
���������� ![]() ��
�� ![]() ��1��
��1�� ![]() ��
��
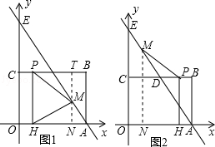
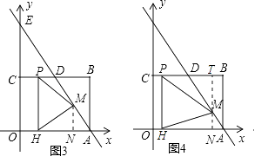
����������1���ɾ��ε����ʿ����C������꣬��B��C����������y= ![]() x2+bx+c���b��c��ֵ���ɸ������߽���ʽ����ֱ��AD�Ľ���ʽΪy=k1x+b1��A��4��0����D��2��3���������һ�κ����Ľ���ʽ�����������κ�����һ�κ����Ľ���ʽ�������F������ꣻ��2��������CF��x����H�䣬��H����BC�Ĵ��߽�BC��P�䣬��P�˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С���ڹ�M��MN��OA��OA��N���ٷֱ����۵�PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ���PH=PMʱ��������������tֵ���ɣ�
x2+bx+c���b��c��ֵ���ɸ������߽���ʽ����ֱ��AD�Ľ���ʽΪy=k1x+b1��A��4��0����D��2��3���������һ�κ����Ľ���ʽ�����������κ�����һ�κ����Ľ���ʽ�������F������ꣻ��2��������CF��x����H�䣬��H����BC�Ĵ��߽�BC��P�䣬��P�˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С���ڹ�M��MN��OA��OA��N���ٷֱ����۵�PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ���PH=PMʱ��������������tֵ���ɣ�
�����㾫����ͨ������������������ε����ʣ����ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������μ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
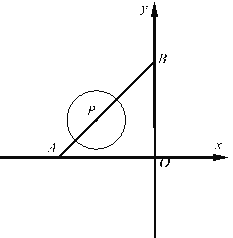
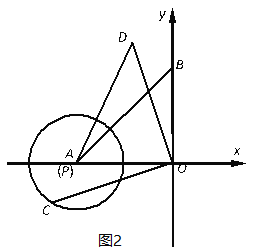
����Ŀ����ͼ1��ֱ��![]() �ֱ�x�ᡢy����A��B���㣬��P���߶�AB�ϵ�һ���㣬��PΪԲ�ģ�rΪ�뾶��Բ��
�ֱ�x�ᡢy����A��B���㣬��P���߶�AB�ϵ�һ���㣬��PΪԲ�ģ�rΪ�뾶��Բ��
��1������P�ĺ�����Ϊ��3������P��x������ʱ����뾶rΪ ����ʱ��P��y���λ�ù�ϵ�� .��ֱ��д�����
��2����![]() ������P������������ֻ��3��������ʱ�����P������.
������P������������ֻ��3��������ʱ�����P������.
��3����ͼ2����Բ��P��A�غϣ�![]() ʱ�����CΪ��P�ϵ�һ�����㣬����OC�����߶�OC�Ƶ�O˳ʱ����ת90�����õ��߶�OD������AD����AD������ֵ��ֱ��д����Ӧ�ĵ�D�����꣮
ʱ�����CΪ��P�ϵ�һ�����㣬����OC�����߶�OC�Ƶ�O˳ʱ����ת90�����õ��߶�OD������AD����AD������ֵ��ֱ��д����Ӧ�ĵ�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ24���ף��ס���������ͬʱ�Ӷ���A����������2����/����ٶ��������εı߰�˳ʱ�뷽���ƶ�������4����/����ٶ��������εı߰���ʱ�뷽���ƶ���ÿ����������ҵ��ٶȾ�����1����/���Ҷ��ı�ԭ�����ƶ�������Ĵ�����ʱ�����������ľ�����______���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD�������������µ���������AB��40�ף�AB���е�ΪP������B���Ĵ�ֱ�߶�Ϊ6�ף��罭������������Ȼ�´����Ƴ��������Σ�Ϊ�˱�֤������ֻ�İ�ȫ�������´�����͵���ĸ߶Ȳ�������30�ף���֪�����ھ�����B����50�ĵ���E��ǡ�ÿ�����E��P��C��һֱ���ϣ�������ǰ��150��ӵ���F��ǡ�ÿ�����F��A��C��һֱ���ϣ�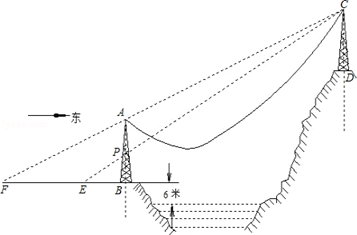
��1��������������ľ��루��ֱ��AB��CD��ľ��룩��
��2�����Ե�AΪ����ԭ�㣬��ˮƽ����Ϊx�ᣬȡ��λ����Ϊ1�ף�BA���ӳ�����Ϊy�Ὠ������ϵ����պ�������߶�Ҫ�����������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ���У����е��ı��ζ��������Σ����е������ζ���ֱ�������Σ��������������εı߳�Ϊ7cm�������������ε�����ĺ��ǣ� ��cm2
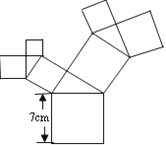
A. 28 B. 49 C. 98 D. 147
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Сѧ���������ᳫ��2+2�����ʽ������ڿ�չ�ļ�������ȡ�����ش�ɹ���С���Ա�ѧ��ȫ��50��ͬѧ��ѡ��Ļ��Ŀ������ͳ�ƣ������ռ��������������±���
1�������Ʊ����е����ݣ�

2���������������е������ٷֱȣ����ƺ��ʵ�ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������20ǧ�ף��ס������˶���A��ȥB�أ�ͼ������l1��l2�ֱ��ʾ�ס�����������·��s��ǧ�ף���ʱ��t��Сʱ��֮��Ĺ�ϵ��
����˵����
����������1Сʱ��
���ҳ���3Сʱ���ϼף�
�ۼ��ٶ���4ǧ��/Сʱ���ҵ��ٶ���6ǧ��/Сʱ��
�����ȵ���B�أ�������ȷ�ĸ����ǣ�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M���߶�AB�е㣬AD��BC���ڵ�N������AC��BD��MC��MD����l=��2����3=��4��
��1����֤����AMD�ա�BMC��
��2��ͼ���ڲ������µ���ĸ������£���д����������AMD�ա�BMC�����������ȫ�������Σ���ѡ������һ�Խ���֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
3��![]() =3��
=3��![]() ��
��
����![]() ����6=����
����6=����![]() ����6��
����6��
����0.5��������1��=����0.5��������1��
����������Щ��ʽ��ӳ�Ĺ��ɣ�����������⣺
(1)�����ʽ��ӳ�Ĺ������������Կ����������£�����������������ʹ���������������IJ����
�� ����
(2)�������������ɵ���������������һ������![]() ������һ����������
������һ����������
(3)������������������ĸa��b��ʾ���������ʽ��ӳ�Ĺ�������ĸ��ʾΪ�� ����
(4)��(3)�еĹ�ϵʽ�У���ĸa��b�Ƿ���Ҫ����һ��������������Ҫ��ֱ��д����ĸa��bӦ�����������������Ҫ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com