
【题目】观察下列等式:
3﹣![]() =3×
=3×![]() ;
;
(﹣![]() )﹣6=(﹣
)﹣6=(﹣![]() )×6;
)×6;
(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根据上面这些等式反映的规律,解答下列问题:
(1)上面等式反映的规律用文字语言可以描述如下:存在两个有理数,使得这两个有理数的差等于
.
(2)若满足上述规律的两个有理数中有一个数是![]() ,求另一个有理数;
,求另一个有理数;
(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为 ;
(4)在(3)中的关系式中,字母a、b是否需要满足一定的条件?若需要,直接写出字母a、b应满足的条件;若不需要,请说明理由.
【答案】(1)它们的积;(2)2或![]() ; (3)a-b=ab;(4)字母a,b应满足的条件是倒数的差是1.
; (3)a-b=ab;(4)字母a,b应满足的条件是倒数的差是1.
【解析】
(1)根据等式反映的规律用文字语言描述即可;
(2)根据规律求解即可;
(3)根据规律求解即可;
(4)根据等式的性质可得![]() =1,即字母a、b应满足的条件是倒数的差是1,依此求解即可.
=1,即字母a、b应满足的条件是倒数的差是1,依此求解即可.
(1)上面等式反映的规律用文字语言可描述为:存在两个有理数,使得这两个有理数的差等于它们的积,
故答案为:它们的积;
(2)∵2-![]() =2×
=2×![]() ,
,
∴另一个有理数为2;
(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为a-b=ab;
(4)a-b=ab,
![]() ,
,
![]() =1,
=1,
故字母a、b应满足的条件是倒数的差是1.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y= ![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= ![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒 ![]() 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示. 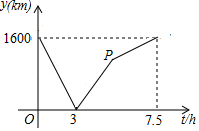
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km?
查看答案和解析>>
科目:初中数学 来源: 题型:
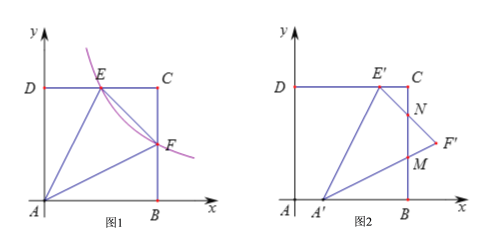
【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系![]() 反比例函数
反比例函数![]() 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.
(1)求证:![]() ;
;
(2)若![]() 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;
(3)在(2)的条件下,将![]() 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到![]() ,如图2,线段
,如图2,线段![]() 与
与![]() 相交于点M,线段
相交于点M,线段![]() 与BC相交于点N.求
与BC相交于点N.求![]() 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图(1),在数轴上A示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB=b-a.
![]()
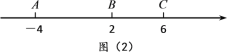
解决问题:如图(2),数轴上点A表示的数是-4,点B表示的数是2,点C表示的数是6.
(1)若数轴上有一点D,且AD=3,求点D表示的数;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.求点A表示的数(用含t的代数式表示),BC等于多少(用含t的代数式表示).
(3)请问:3BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
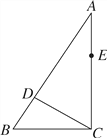
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商家常将两种糖混合成“什锦糖”出售.对“什锦糖”的定价用以下方法确定:
若A种糖的单价为a元/千克,B种糖的单价为b元/千克(a≠b),则m千克的A种糖与n千克的B种糖混合而成的“什锦糖”单价为![]() 元.
元.
(1)当a=20,b=30时,
①将10千克的A种糖与15千克的B种糖混合而成的“什锦糖”单价为多少?
②在①的基础上,若要将“什锦糖”单价提高2元,则需增加B种糖多少千克?
(2)若现有两种“什锦糖”:一种是由10千克的A种糖和10千克的B种糖混合而成,另一种是由100元价值的A种糖和100元价值的B种糖混合而成,则这两种“什锦糖”的单价哪一种更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com