练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】重庆市中小学教育大力提倡“2+2”素质教育，在开展的几年来，取得了重大成果．小明对本学期全班50名同学所选择的活动项目进行了统计，根据收集的数据制作了下表：

    1）请完善表格中的数据：

    2）根据上述表格中的人数百分比，绘制合适的统计图．

    【答案】(1）见解析；(2）见解析.

    【解析】

    （1）由题意可求出科技创作的人数;用体育技能人数、艺术特长人数分别除以总人数求出所占的百分率,根据求出的数据填表即可.

    (2)根据各选项人数所占的百分率,求出所对应的圆心角的度数,即可画出扇形统计图.

    解：1）50﹣25﹣10=15，科技创作的人数为15人，

    25÷50×100%=50%，

    艺术特长的人数所占的百分比为10÷50×100%=20%，

    艺术特长的人数所占的百分比为20%；

    2）绘制扇形统计图如右．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+3与x轴的两个交点分别为（m，0）和（n，0），则当x=m+n时，y的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

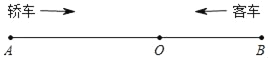
    【题目】如图，A，B两地相距450千米，两地之间有一个加油站O，且AO＝270千米，一辆轿车从A地出发，以每小时90千米的速度开往B地，一辆客车从B地出发，以每小时60千米的速度开往A地，两车同时出发，设出发时间为t小时．

    （1）经过几小时两车相遇？

    （2）当出发2小时时，轿车和客车分别距离加油站O多远？

    （3）经过几小时，两车相距50千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，OM是∠AOC的角平分线，ON是∠BOC的角平分线．

    （1）当∠AOB=90°，∠BOC=40°时，求∠MON的度数．

    （2）若∠AOB的度数不变，∠BOC的度数为α时，求∠MON的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），在平面直角坐标系中，矩形ABCO，B点坐标为（4，3），抛物线y= x2+bx+c经过矩形ABCO的顶点B、C，D为BC的中点，直线AD与y轴交于E点，与抛物线y= x2+bx+c交于第四象限的F点．

    （1）求该抛物线解析式与F点坐标；
    （2）如图（2），动点P从点C出发，沿线段CB以每秒1个单位长度的速度向终点B运动；同时，动点M从点A出发，沿线段AE以每秒 个单位长度的速度向终点E运动．过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒

    ①问EP+PH+HF是否有最小值？如果有，求出t的值；如果没有，请说明理由．
    ②若△PMH是等腰三角形，请直接写出此时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC=4，AO=BO,P是射线CO上的一个动点，∠AOC=60°,则当△PAB为直角三角形时，AP的长为 __________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（　　）

    A. △AFD≌△DCE B. AF=AD C. AB=AF D. BE=AD﹣DF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知图①中抛物线y=ax2+bx+c经过点D（﹣1，0）、C（0，﹣1）、E（1，0）．
    （1）求图①中抛物线的函数表达式；
    （2）将图①中抛物线向上平移一个单位，再绕原点O顺时针旋转180°后得到图②中抛物线，则图②中抛物线的函数表达式为；
    （3）图②中抛物线与直线y=﹣ x﹣ 相交于A、B两点（点A在点B的左侧），如图③，求点A、B的坐标，并直接写出当一次函数的值大于二次函数的值时，x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：如图（1），在数轴上A示的数为a，B点表示的数为b，则点A到点B的距离记为AB．线段AB的长可以用右边的数减去左边的数表示，即AB＝b－a．

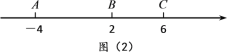
    解决问题：如图（2），数轴上点A表示的数是－4，点B表示的数是2，点C表示的数是6．

    （1）若数轴上有一点D，且AD＝3，求点D表示的数；

    （2）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．求点A表示的数（用含t的代数式表示），BC等于多少（用含t的代数式表示）．

    （3）请问：3BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．

    查看答案和解析>>

    同步练习册答案