
【题目】已知:如图,OM是∠AOC的角平分线,ON是∠BOC的角平分线.
(1)当∠AOB=90°,∠BOC=40°时,求∠MON的度数.
(2)若∠AOB的度数不变,∠BOC的度数为α时,求∠MON的度数.

【答案】(1)45°;(2)45°.
【解析】
(1)第一种方法:先求得∠AOC=130°,然后由角平分线的定义求得∠COM=65°、∠CON=20°,然后根据∠MON=∠COM﹣∠CON求解即可;
第二种方法:分别计算∠BOM和∠BON,根据∠MON=∠BOM+∠BON求解即可;
(2)第一种方法:根据角平分线的定义分别得∠COM=![]() ∠AOC,∠CON=
∠AOC,∠CON=![]() ∠BOC,所以∠MON=∠COM﹣∠CON=
∠BOC,所以∠MON=∠COM﹣∠CON=![]() ∠AOB=45°;
∠AOB=45°;
第二种方法:同(1):根据∠MON=∠COM﹣∠CON求解即可.
(1)(第一种方法)∵∠AOB=90°,∠BOC=40°,∴∠AOC=∠AOB+∠BOC=90°+40°=130°.
∵OM是∠AOC的角平分线,∴∠COM=![]() ∠AOC=65°.
∠AOC=65°.
∵ON是∠BOC的角平分线,∴∠CON=![]() ∠BOC=20°,∴∠MON=∠COM﹣∠CON=65°﹣20°=45°;
∠BOC=20°,∴∠MON=∠COM﹣∠CON=65°﹣20°=45°;
第二种方法:∵∠AOB=90°,∠BOC=40°,∴∠AOC=∠AOB+∠BOC=90°+40°=130°.
∵OM是∠AOC的角平分线,∴∠AOM=![]() ∠AOC=65°.
∠AOC=65°.
∵∠AOB=90°,∴∠BOM=∠AOB﹣∠AOM=90°﹣65°=25°.
又∵ON是∠BOC的角平分线,∠BOC=40°,∴∠BON=![]() ∠BOC=20°,∴∠MON=∠BOM+∠BON=25°+20°=45°;
∠BOC=20°,∴∠MON=∠BOM+∠BON=25°+20°=45°;
(2)(第一种方法)∵OM是∠AOC的角平分线,∴∠COM=![]() ∠AOC.
∠AOC.
∵ON是∠BOC的角平分线,∴∠CON=![]() ∠BOC,∴∠MON=∠COM﹣∠CON=
∠BOC,∴∠MON=∠COM﹣∠CON=![]() ∠AOC﹣
∠AOC﹣![]() ∠BOC=
∠BOC=![]() (∠AOC﹣∠BOC)=
(∠AOC﹣∠BOC)=![]() ∠AOB.
∠AOB.
∵∠AOB=90°,∴∠MON=45°;
(第二种方法)∵∠AOB=90°,∠BOC=α,∴∠AOC=∠AOB+∠BOC=90°+α.
∵OM是∠AOC的角平分线,∴∠COM=![]() ∠AOC=
∠AOC=![]() (90°+α).
(90°+α).
∵ON是∠BOC的角平分线,∠BOC=α,∴∠CON=![]() ∠BOC=
∠BOC=![]() α,∴∠MON=∠COM﹣∠CON=
α,∴∠MON=∠COM﹣∠CON=![]() (90°+α)﹣
(90°+α)﹣![]() α=45°.
α=45°.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
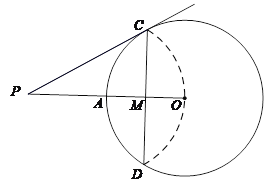
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.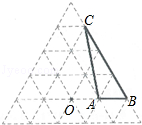
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米.跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米.已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上.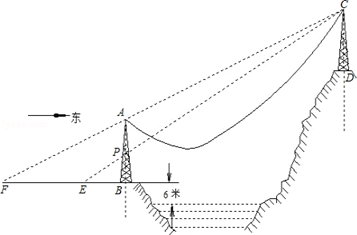
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为x轴,取单位长度为1米,BA的延长方向为y轴建立坐标系.求刚好满足最低高度要求的这个抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市中小学教育大力提倡“2+2”素质教育,在开展的几年来,取得了重大成果.小明对本学期全班50名同学所选择的活动项目进行了统计,根据收集的数据制作了下表:
1)请完善表格中的数据:

2)根据上述表格中的人数百分比,绘制合适的统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
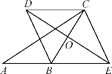
【题目】已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com