
【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.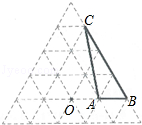
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
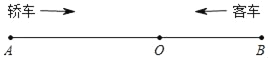
【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
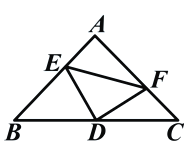
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,OM是∠AOC的角平分线,ON是∠BOC的角平分线.
(1)当∠AOB=90°,∠BOC=40°时,求∠MON的度数.
(2)若∠AOB的度数不变,∠BOC的度数为α时,求∠MON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )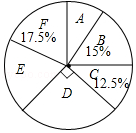
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com