练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，⊙O是△ABC的内切圆，切点为D，E，F,若AD、BE的长为方程的两个根，则△ABC的周长为 ______．

    【答案】40；

    【解析】求△ABC的周长，关键是求出两条直角边的长；由已知的方程可求出AF、BE的长，结合切线长定理和勾股定理，可求得CE、CF的长，进而可求出AC、BC的长；再由勾股定理求得AB，即可求△ABC的周长．

    如图；

    解方程，得：

    x=12，x=5，

    ∴AD=AF=5，BF=BE=12；AB=17,

    设CE=CD=x，则AC=5+x，BC=12+x；

    由勾股定理，得：

    AB2=AC2+BC2,即172=(5+x)2+(12+x)2，

    解得：x=3(负值舍去)，

    ∴AC=8，BC=15；

    因此△ABC的周长=AC+BC+AB=8+15+17=40,.

    故答案为：40.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】列一元一次方程解应用题．

    （1）商店出售茶壶和茶杯，茶壶每只定价20元，茶杯每只定价5元，该商品制定了两种优惠方法：

    ①买一只茶壶赠一只茶杯；②按总价的90%付款．某顾客购买茶壶5只，茶杯若干只（不少于5只），问顾客买多少只茶杯时，两种方法付款相同．假如该顾客买了茶杯20只，哪种买法实惠？

    （2）某人原计划骑车以每小时12千米的速度由A地到B地，这样便可在规定的时间到达，但他因事将原计划出发的时间推迟了20分钟，只好以每小时15千米的速度前进，结果比规定时间早4分钟到达B地，求A，B两地间的距离．

    （3）某工厂完成一批产品，一车间单独完成需30天，二车间单独完成需20天．

    ①如一车间先做若干天，然后由二车间继续做，直至完成，前后共做了25天，问一车间先做了几天？

    ②如一车间先做了3天后，二车间加入一起做，还需多少天才能完成？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市今年的信息技术结业考试，采用学生抽签的方式决定自己的考试内容．规定：每位考生先在三个笔试题（题签分别用代码B1、B2、B3表示）中抽取一个，再在三个上机题（题签分别用代码J1、J2、J3表示）中抽取一个进行考试．小亮在看不到题签的情况下，分别从笔试题和上机题中随机地抽取一个题签．
    （1）用树状图或列表法表示出所有可能的结果；
    （2）求小亮抽到的笔试题和上机题的题签代码的下标（例如“B1”的下标为“1”）为一个奇数一个偶数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

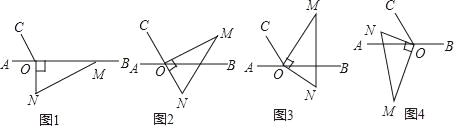
    【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°，将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

    （1）将图1中的三角尺绕点O逆时针旋转至图2，使点N在OC的反向延长线上，请直接写出图中∠MOB的度数；

    （2）将图1中的三角尺绕点O逆时针旋转至图3，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；

    （3）将图1中的三角尺绕点O顺时针旋转至图4，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD中，∠B=60°，点E在边BC上，点F在边CD上．若EB=2，DF=3，∠EAF=60°，则△AEF的面积等于 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

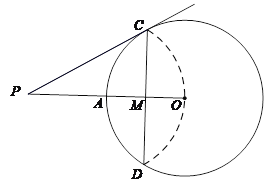
    【题目】如图，已知⊙O的半径为4，OA为半径，CD为弦，OA与CD交于点M，将弧CD沿着CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC.

    （1）求CD的长；

    （2）求证：PC是⊙O的切线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

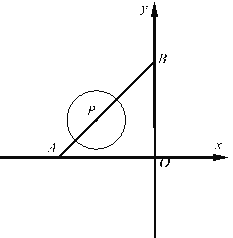
    【题目】如图1，直线分别交x轴、y轴于A、B两点，点P是线段AB上的一动点，以P为圆心，r为半径画圆．

    （1）若点P的横坐标为﹣3，当⊙P与x轴相切时，则半径r为 ，此时⊙P与y轴的位置关系是 .（直接写结果）

    （2）若，当⊙P与坐标轴有且只有3个公共点时，求点P的坐标.

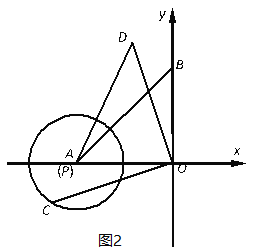
    （3）如图2，当圆心P与A重合，时，设点C为⊙P上的一个动点，连接OC，将线段OC绕点O顺时针旋转90°，得到线段OD，连接AD，求AD长的最值并直接写出对应的点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．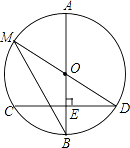
    （1）若BE=8，求⊙O的半径；
    （2）若∠DMB=∠D，求线段OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB、CD是两个过江电缆的铁塔，塔AB高40米，AB的中点为P，塔底B距江面的垂直高度为6米．跨江电缆因重力自然下垂近似成抛物线形，为了保证过往船只的安全，电缆下垂的最低点距江面的高度不得少于30米．已知：人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上；再向西前进150米后从地面F点恰好看到点F、A、C在一直线上．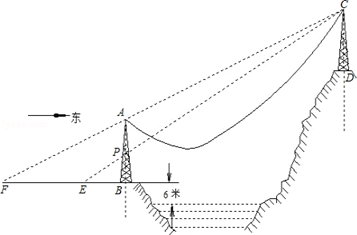

    （1）求两铁塔轴线间的距离（即直线AB、CD间的距离）；
    （2）若以点A为坐标原点，向东的水平方向为x轴，取单位长度为1米，BA的延长方向为y轴建立坐标系．求刚好满足最低高度要求的这个抛物线的解析式．

    查看答案和解析>>

    同步练习册答案