
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数;
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
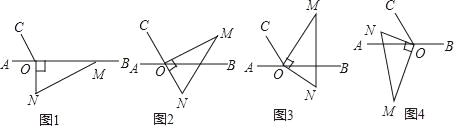
【答案】(1)30°;(2)150°;(3)∠AOM﹣∠NOC=30°,理由见解析
【解析】
(1) 根据对顶角求出∠BON,代入∠BOM=∠MON-∠BON求出即可;
(2) 求出么BOC=![]() , 根据角平分线定义请求出∠COM=∠BOM=
, 根据角平分线定义请求出∠COM=∠BOM=![]() , 代入∠CON=∠MON+∠COM求出即可;
, 代入∠CON=∠MON+∠COM求出即可;
(3)用∠AOM和∠CON表示出∠AON,然后列出方程整理即可得解.
(1)如图2,∵∠AOC=60°,
∴∠BON=∠AOC=60°,
∵∠MON=90°,
∴∠BOM=∠MON﹣∠BON=30°,
(2)∵∠AOC=60°,
∴∠BOC=180°﹣∠AOC=120°,
∵OM平分∠BOC,
∴∠COM=∠BOM=60°,
∵∠MON=90°,
∴∠CON=∠MON+∠COM=90°+60°=150°;
(3)∠AOM﹣∠NOC=30°,
理由是:∵∠MON=90°,∠AOC=60°,
∴∠AON=90°﹣∠AOM,
∠AON=60°﹣∠NOC,
∴90°﹣∠AOM=60°﹣∠NOC,
∴∠AOM﹣∠NOC=30°,
故∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第6个小房子用的石子数量为 ( )

A. 87 B. 77 C. 70 D. 60
查看答案和解析>>
科目:初中数学 来源: 题型:
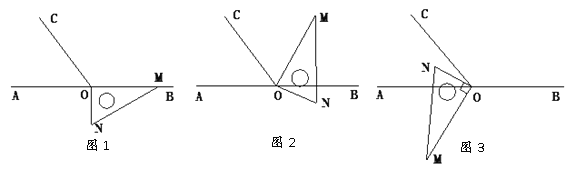
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在y轴的正半轴上,点A在x轴的正半轴上,点C的坐标为(0,8),将△ABC沿直线AB折叠,点C落在x轴的负半轴D(﹣4,0)处.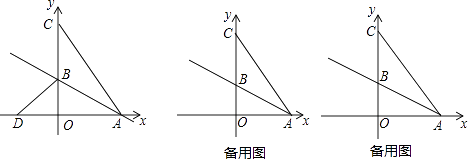
(1)求直线AB的解析式;
(2)点P从点A出发以每秒4 ![]() 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);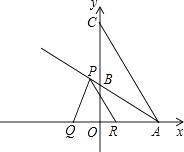
(3)在(2)的条件下,点N是射线AB上一点,以点N为圆心,同时经过R、Q两点作⊙N,⊙N交y轴于点E,F.是否存在t,使得EF=RQ?若存在,求出t的值,并求出圆心N的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校允许学生在同个系列的校服里选择不同款式,新生入学后,学校就新生对校服款式选择情况作了抽样调查,调查分为款式A、B、C、D四种,每位新生只能选择一种款式,现将调查统计结果制成了如下两幅不完整的统计图,请结合这两幅统计图,回答下列问题:
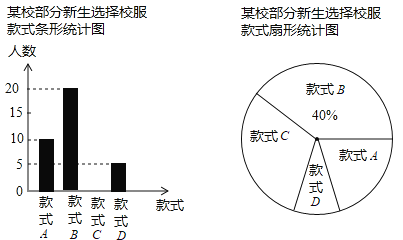
(1)在本次调查中,一共抽取了多少名新生,并补全条形统计图;
(2)若该校有847名新生,服装厂已生产了270套B款式的校服,请你按相关统计知识判断是否还要继续生产B款式的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
查看答案和解析>>
科目:初中数学 来源: 题型:
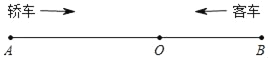
【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com