
【题目】在正常情况下,某出租车司机每天驾车行驶![]() 小时,且平均速度为
小时,且平均速度为![]() 千米时。已知他在A日比正常情况少行驶2小时,平均速度比正常情况慢5千米/时,他在B日比正常情况多行驶2小时,平均速度比正常情况快5千米/时,
千米时。已知他在A日比正常情况少行驶2小时,平均速度比正常情况慢5千米/时,他在B日比正常情况多行驶2小时,平均速度比正常情况快5千米/时,
(1)问A日出租车司机比正常情况少行驶多少千米?(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)已知A日出租车司机比正常情况少行驶120千米,求B日出租车司机比正常情况多行驶多少千米.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),以
重合),以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() .
.
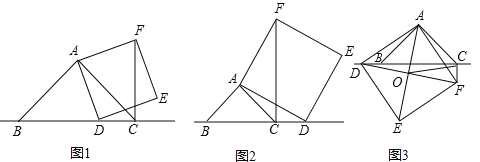
(1)如图1,当点![]() 在线段
在线段![]() 上时,请直接写出:
上时,请直接写出:![]() ,
,![]() ,
,![]() 三条线段之间的数量关系为________.
三条线段之间的数量关系为________.
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,其他条件不变.(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请你写出正确的结论,并给出证明.
的延长线上时,其他条件不变.(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请你写出正确的结论,并给出证明.
(3)如图3,当点![]() 在线段
在线段![]() 的反向延长线上时,且点
的反向延长线上时,且点![]() ,
,![]() 分别在直线
分别在直线![]() 的两侧,其他条件不变.请直接写出:
的两侧,其他条件不变.请直接写出:![]() ,
,![]() ,
,![]() 三条线段之间的数量关系______________.
三条线段之间的数量关系______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )

A. △CDF≌△EBC
B. ∠CDF=∠EAF
C. CG⊥AE
D. △ECF是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 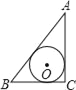 B.
B. 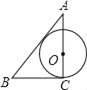 C.
C. 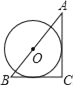 D.
D. 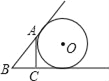
查看答案和解析>>
科目:初中数学 来源: 题型:
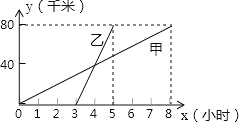
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)谁先出发早多长时间谁先到达B地早多长时间?
(2)两人在途中的速度分别是多少?
(3)分别求出表示甲、乙在行驶过程中的路程与时间之间的函数关系式(不要求写出自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
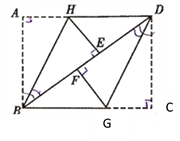
【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
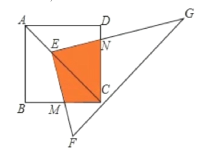
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为6,则重叠部分四边形EMCN的面积为( )
A. 9B. 12C. 16D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,过程如下,请补充完整.
的图象和性质进行了探究,过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | … |
其中,![]() __________.
__________.
(2)根据上表的数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
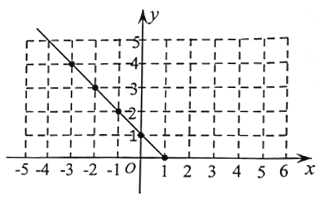
(3)观察图象,写出该函数的两条性质:
①____________________________________________________________
②____________________________________________________________
(4)进一步探究函数图象发现:
①方程![]() 的解是__________.
的解是__________.
②方程![]() 的解是__________.
的解是__________.
③关于![]() 的方程
的方程![]() 有两个不相等实数根,则
有两个不相等实数根,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com