
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨º«
÷–£¨º«![]() ”Î
”Î![]() µƒ∫Ø ˝
µƒ∫Ø ˝![]() £®
£®![]() °Ÿ0£¨n°Ÿ0£©µƒÕºœÛŒ™Õº–ŒG, “—÷™Õº–ŒG”Î
°Ÿ0£¨n°Ÿ0£©µƒÕºœÛŒ™Õº–ŒG, “—÷™Õº–ŒG”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨µ±
£¨µ±![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() ”–◊Ó–°£®ªÚ◊Ó¥Û£©÷µn, µ„Bµƒ◊¯±ÍŒ™(
”–◊Ó–°£®ªÚ◊Ó¥Û£©÷µn, µ„Bµƒ◊¯±ÍŒ™(![]() ,
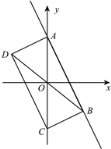
, ![]() )£¨µ„A°¢Bπÿ”⁄‘≠µ„Oµƒ∂‘≥∆µ„∑÷±Œ™C°¢D£¨»ÙA°¢B°¢C°¢D÷–»Œ∫Œ»˝µ„∂º≤ª‘⁄“ª÷±œfl…œ£¨«“∂‘Ω«œflAC£¨BDµƒΩªµ„”Α≠µ„O÷ÿ∫œ£¨‘Ú≥∆Àƒ±fl–ŒABCDŒ™Õº–ŒGµƒ∞ÈÀÊÀƒ±fl–Œ£¨÷±œflABŒ™Õº–ŒGµƒ∞ÈÀÊ÷±œfl.
)£¨µ„A°¢Bπÿ”⁄‘≠µ„Oµƒ∂‘≥∆µ„∑÷±Œ™C°¢D£¨»ÙA°¢B°¢C°¢D÷–»Œ∫Œ»˝µ„∂º≤ª‘⁄“ª÷±œfl…œ£¨«“∂‘Ω«œflAC£¨BDµƒΩªµ„”Α≠µ„O÷ÿ∫œ£¨‘Ú≥∆Àƒ±fl–ŒABCDŒ™Õº–ŒGµƒ∞ÈÀÊÀƒ±fl–Œ£¨÷±œflABŒ™Õº–ŒGµƒ∞ÈÀÊ÷±œfl.

£®1£©»ÁÕº£¨»Ù∫Ø ˝![]() µƒÕºœÛº«Œ™Õº–ŒG£¨«ÛÕº–ŒGµƒ∞ÈÀÊ÷±œflµƒ±Ì¥Ô Ω£ª
µƒÕºœÛº«Œ™Õº–ŒG£¨«ÛÕº–ŒGµƒ∞ÈÀÊ÷±œflµƒ±Ì¥Ô Ω£ª
£®2£©»ÁÕº£¨»ÙÕº–ŒGµƒ∞ÈÀÊ÷±œflµƒ±Ì¥Ô Ω «![]() £¨«“∞ÈÀÊÀƒ±fl–Œµƒ√ʪ˝Œ™12£¨«Û
£¨«“∞ÈÀÊÀƒ±fl–Œµƒ√ʪ˝Œ™12£¨«Û![]() ”Î
”Î![]() µƒ∫Ø ˝
µƒ∫Ø ˝![]() £®m£æ0£¨n £º0£©µƒ±Ì¥Ô Ω£ª
£®m£æ0£¨n £º0£©µƒ±Ì¥Ô Ω£ª
£®3£©»ÁÕº£¨»ÙÕº–ŒGµƒ∞ÈÀÊ÷±œfl «![]() £¨«“∞ÈÀÊÀƒ±fl–ŒABCD «æÿ–Œ£¨«Ûµ„Bµƒ◊¯±Í.
£¨«“∞ÈÀÊÀƒ±fl–ŒABCD «æÿ–Œ£¨«Ûµ„Bµƒ◊¯±Í.
°æ¥∞∏°ø£®1£©![]() £®2£©
£®2£©![]() £®3£©
£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©œ»¿˚”√≈◊ŒÔœflΩ‚Œˆ Ω»∑∂®Aµ„∫ÕBµ„◊¯±Í£¨»ª∫Û¿˚”√¥˝∂®œµ ˝∑®«Û∞ÈÀÊ÷±œflµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº2£¨◊˜BE°ÕAC”⁄µ„E£¨¿˚”√“ª¥Œ∫Ø ˝Ω‚Œˆ Ω∫Õπÿ”⁄‘≠µ„∂‘≥∆µƒ◊¯±ÍÃÿ’˜µ√µΩA£®0£¨-3£©∫ÕC£®0£¨3£©£¨‘Ÿ¿˚”√∆Ω––Àƒ±fl–ŒABCDµƒ√ʪ˝Œ™12ø…«Û≥ˆBE=2£¨‘ÚBµ„µƒ∫·◊¯±ÍŒ™2£¨‘Ú¿˚”√∂•µ„B‘⁄÷±œfl![]() …œµ√µΩ∂•µ„Bµƒ◊¯±ÍŒ™£®2£¨-1£©£¨‘Ú…Ë∂•µ„ Ωy=a£®x-2£©2-1£¨»ª∫Û∞—Aµ„◊¯±Í¥˙»Î«Û≥ˆaº¥ø…µ√µΩ≈◊ŒÔœflΩ‚Œˆ Ω£ª
…œµ√µΩ∂•µ„Bµƒ◊¯±ÍŒ™£®2£¨-1£©£¨‘Ú…Ë∂•µ„ Ωy=a£®x-2£©2-1£¨»ª∫Û∞—Aµ„◊¯±Í¥˙»Î«Û≥ˆaº¥ø…µ√µΩ≈◊ŒÔœflΩ‚Œˆ Ω£ª
£®3£©»ÁÕº£¨◊˜![]() ÷·”⁄µ„
÷·”⁄µ„![]() ,”…
,”…![]() ‘⁄÷±œfl
‘⁄÷±œfl![]() …œ£¨ø…µ√µ„Bµƒ◊¯±ÍŒ™£®
…œ£¨ø…µ√µ„Bµƒ◊¯±ÍŒ™£®![]() £¨
£¨![]() £©£¨‘⁄Rt°˜OEB÷–£¨”…π¥π…∂®¿Ì«Û≥ˆmµƒ÷µ£¨¥”∂¯ø…«Û≥ˆµ„Bµƒ◊¯±Í.
£©£¨‘⁄Rt°˜OEB÷–£¨”…π¥π…∂®¿Ì«Û≥ˆmµƒ÷µ£¨¥”∂¯ø…«Û≥ˆµ„Bµƒ◊¯±Í.
£®1£©”…“‚µ√![]()
![]() £¨
£¨
…ËÀ˘«Û∞ÈÀÊ÷±œflµƒ±Ì¥Ô ΩŒ™![]() £¨
£¨
‘Ú![]()
Ω‚£¨µ√![]()
À˘“‘∫Ø ˝y=£®x-2£©2+1µƒ∞ÈÀÊ÷±œflµƒ±Ì¥Ô Ω «![]() £ª
£ª
£®2£©»ÁÕº£¨◊˜BE°ÕAC”⁄µ„E,
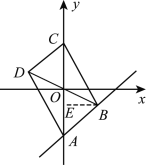
”…“‚÷™£¨
OC=OA£¨OB=OD£¨
°‡Àƒ±fl–ŒABCD «∆Ω––Àƒ±fl–Œ.
°fl![]() £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨
°fl∆Ω––Àƒ±fl–ŒABCDµƒ√ʪ˝Œ™12£¨
°‡![]() £¨
£¨
º¥![]() ,
,
°‡![]() £¨
£¨
°fl![]() £æ0£¨º¥∂•µ„B‘⁄
£æ0£¨º¥∂•µ„B‘⁄![]() ÷·µƒ”“≤‡£¨«“‘⁄÷±œfl
÷·µƒ”“≤‡£¨«“‘⁄÷±œfl![]() …œ£¨
…œ£¨
°‡![]() £¨
£¨
”÷Õº–ŒGæ≠π˝µ„![]() ,
,
…Ë∂•µ„ Ωy=a£®x-2£©2-1£¨
°‡4a=-2£¨
![]() £¨
£¨
![]() £ª
£ª
£®3£©»ÁÕº£¨◊˜![]() ÷·”⁄µ„
÷·”⁄µ„![]() ,
,
”…“—÷™µ√£∫![]() £¨
£¨![]() £¨
£¨
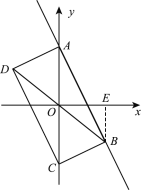
°fl![]() ‘⁄÷±œfl
‘⁄÷±œfl![]() …œ£¨
…œ£¨
°‡![]() £¨º¥µ„Bµƒ◊¯±ÍŒ™£®
£¨º¥µ„Bµƒ◊¯±ÍŒ™£®![]() £¨
£¨![]() £©£¨
£©£¨
°flæÿ–Œ![]() £¨
£¨
°‡![]() = 4£¨
= 4£¨
°‡![]() £¨
£¨
‘⁄Rt°˜OEB÷–
![]() £¨
£¨
°‡![]() £¨
£¨
°‡£®≤ª∫œÃ‚“‚£¨…·»•£©£¨
![]() £¨
£¨
°‡![]() £¨
£¨
°‡µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() .
.


 √˚–£¡™√ÀøÏ¿÷øŒÃ√œµ¡–¥∞∏
√˚–£¡™√ÀøÏ¿÷øŒÃ√œµ¡–¥∞∏ ª∆∏‘¥¥”≈æÌœµ¡–¥∞∏
ª∆∏‘¥¥”≈æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÕ¯¬Á ”∆µµƒ–À∆»√÷ÿ«Ï“ª∂»≥…Œ™°∞Õ¯∫Ï°±≥« –£¨≤¢«“ πµ√µΩ…Ω≥«÷ÿ«Ïµƒ”ŒøÕæÁ‘ˆ.ƒ≥¬√”Œπ´Àæ∏˘æ›”ŒøÕµƒ–Ë«ÛÕ∆≥ˆ¡À°∞øÏÀŸ”Œ°±∫Õ°∞æ´∆∑”Œ°±¡Ω÷÷Ã◊≤Õ.9‘¬∑›£¨∏√¬√”Œπ´Àæ°∞øÏÀŸ”Œ°±.°∞æ´∆∑”Œ°±¡Ω÷÷Ã◊≤Õµƒº€∏Ò∑÷±Œ™800‘™/»À.2000‘™/»À£¨∆‰÷–°∞øÏÀŸ”Œ°±Ã◊≤Õµƒ”ŒøÕ»À ˝±»°∞æ´∆∑”Œ°±Ã◊≤Õµƒ”ŒøÕ»À ˝µƒ2±∂∂‡300»À£¨◊‹ ’»Î «240ÕÚ‘™.
(1)«Û9‘¬∑›∏√¬√”Œπ´Àæ°∞øÏÀŸ”Œ°±Ã◊≤Õµƒ”ŒøÕ»À ˝£ª
(2)∏√π´À挙¡ÀΩ”ƒ…∏¸∂‡µƒ”ŒøÕ£¨Ã·…˝ø⁄±Æ£¨10‘¬∑›°∞øÏÀŸ”Œ°±Ã◊≤Õº€∏Ò±»9‘¬∑›œ¬Ωµ¡À![]() £¨10‘¬∑›°∞æ´∆∑”Œ°±Ã◊≤Õº€∏Ò±»9‘¬∑›œ¬Ωµ¡À
£¨10‘¬∑›°∞æ´∆∑”Œ°±Ã◊≤Õº€∏Ò±»9‘¬∑›œ¬Ωµ¡À![]() .“—÷™10‘¬∑›∏√π´Àæ¡Ω÷÷Ã◊≤Õµƒ”ŒøÕ»À ˝µƒ∫Õ¥ÔµΩ4000»À£¨∆‰÷–°∞æ´∆∑”Œ°±Ã◊≤Õµƒ”ŒøÕ»À ˝’º¡Ω÷÷Ã◊≤Õµƒ”ŒøÕ»À ˝µƒ∫Õµƒ
.“—÷™10‘¬∑›∏√π´Àæ¡Ω÷÷Ã◊≤Õµƒ”ŒøÕ»À ˝µƒ∫Õ¥ÔµΩ4000»À£¨∆‰÷–°∞æ´∆∑”Œ°±Ã◊≤Õµƒ”ŒøÕ»À ˝’º¡Ω÷÷Ã◊≤Õµƒ”ŒøÕ»À ˝µƒ∫Õµƒ![]() £¨«“10‘¬∑›◊‹ ’»Î¥ÔµΩ¡À457.6ÕÚ‘™£¨«Ûaµƒ÷µ
£¨«“10‘¬∑›◊‹ ’»Î¥ÔµΩ¡À457.6ÕÚ‘™£¨«Ûaµƒ÷µ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
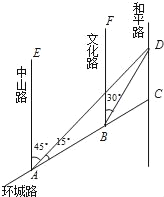
°æƒø°ø»ÁÕº£¨AC «ƒ≥ –ª∑≥«¬∑µƒ“ª∂Œ£¨AE£¨BF£¨CD∂º «ƒœ±±∑ΩœÚµƒΩ÷µ¿£¨∆‰”Ϊ∑≥«¬∑ACµƒΩª≤ʬ∑ø⁄∑÷± «A£¨B£¨C£Ææ≠≤‚¡øª®ª‹ ¿ΩÁDŒª”⁄µ„Aµƒ±±∆´∂´45°„∑ΩœÚ£¨µ„Bµƒ±±∆´∂´30°„∑ΩœÚ…œ£¨AB=2km£¨°œDAC=15°„£Æ
£®1£©«ÛB£¨D÷ƺ‰µƒæ‡¿Î£ª
£®2£©«ÛC£¨D÷ƺ‰µƒæ‡¿Î£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
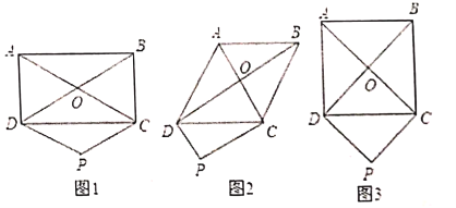
°æƒø°ø£®1£©»ÁÕºæÿ–Œ![]() µƒ∂‘Ω«œfl
µƒ∂‘Ω«œfl![]() .
.![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() £¨«“
£¨«“![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨≈–∂œÀƒ±fl–Œ
£¨≈–∂œÀƒ±fl–Œ![]() µƒ–Œ◊¥≤¢Àµ√˜¿Ì”….
µƒ–Œ◊¥≤¢Àµ√˜¿Ì”….
£®2£©»Áπ˚ƒø÷–µƒæÿ–Œ±‰Œ™¡‚–Œ£¨Àƒ±fl–Œ![]() µƒ–Œ◊¥____________.
µƒ–Œ◊¥____________.
£®3£©»Áπ˚ƒø÷–µƒæÿ–Œ±‰Œ™’˝∑Ω–Œ£¨Àƒ±fl–Œ![]() µƒ–Œ◊¥____________.
µƒ–Œ◊¥____________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
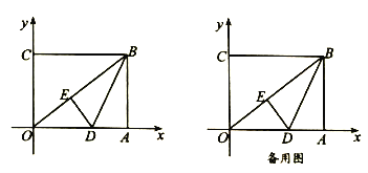
°æƒø°ø”–’‚—˘“ª∏ˆŒ Â:ÃΩæø∫Ø ˝![]() µƒÕºœÛ”Ζ‘÷ .–°∂´∏˘æ›—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝
µƒÕºœÛ”Ζ‘÷ .–°∂´∏˘æ›—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝![]() µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø.
µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø.
œ¬√Ê «–°∂´µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚:
(1)∫Ø ˝![]() µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß « ;
µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß « ;
(2)œ¬±Ì «y”Îxµƒº∏◊È∂‘”¶÷µ.
x | °≠ | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | °≠ |
y | °≠ |
|
|
|
| 3 |
|
|
| m | °≠ |
«Ûmµƒ÷µ;
(3)»Áœ¬Õº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨√Ë≥ˆ¡À“‘…œ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„.∏˘æ›√Ë≥ˆµƒµ„£¨ª≠≥ˆ∏√∫Ø ˝µƒÕºœÛ;

(4)Ω·∫œ∫Ø ˝µƒÕºœÛ£¨–¥≥ˆ∏√∫Ø ˝µƒ“ªÃı–‘÷ : .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ª∏ˆ‘≤÷˘ÃÂ∞¸◊∞∫–£¨∏fl40cm£¨µ◊√Ê÷‹≥§20cm£Æœ÷Ω´≤ …´æÿ–Œ÷Ω¥¯AMCN≤√ºÙ≥…“ª∏ˆ∆Ω––Àƒ±fl–ŒABCD£®»ÁÕº1£©£¨»ª∫Û”√’‚Ãı∆Ω––Àƒ±fl–Œ÷Ω¥¯∞¥»ÁÕº2µƒ∑Ω Ω∞—’‚∏ˆ‘≤÷˘ÃÂ∞¸◊∞∫–µƒ≤‡√ÊΩ¯––∞¸Ã˘£®“™«Û∞¸Ã˘ ±√ª”–÷ÿµ˛≤ø∑÷£©£¨÷Ω¥¯‘⁄≤‡√Ê≤¯»∆Àƒ»¶£¨’˝∫√Ω´’‚∏ˆ‘≤÷˘ÃÂ∞¸◊∞∫–µƒ≤‡√Ê»´≤ø∞¸Ã˘¬˙£¨‘ÚÀ˘–˵ƒ÷Ω¥¯ADµƒ≥§∂»Œ™_____ cm£Æ
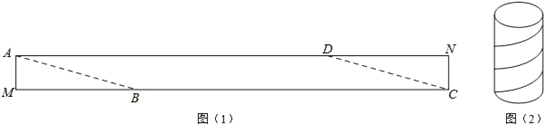
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨AB£ΩAC£¨“‘ABŒ™÷±æ∂µƒ°—O∑÷±”ÎBC°¢ACΩª”⁄µ„D°¢E£¨π˝µ„D◊˜°—Oµƒ«–œflDF£¨ΩªAC”⁄µ„F£Æ
£®1£©«Û÷§£∫DF°ÕAC£ª
£®2£©»Ù°—Oµƒ∞Îæ∂Œ™4£¨°œCDF£Ω22.5°„£¨«Û“ı”∞≤ø∑÷µƒ√ʪ˝£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨![]() Œ™◊¯±Í‘≠µ„£¨æÿ–Œ
Œ™◊¯±Í‘≠µ„£¨æÿ–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() °¢
°¢![]() £¨Ω´æÿ–Œ
£¨Ω´æÿ–Œ![]() µƒ“ª∏ˆΩ«
µƒ“ª∏ˆΩ«![]() —ÿ÷±œfl
—ÿ÷±œfl![]() ’€µ˛£¨ πµ√µ„
’€µ˛£¨ πµ√µ„![]() ¬‰‘⁄∂‘Ω«œfl
¬‰‘⁄∂‘Ω«œfl![]() …œµƒµ„
…œµƒµ„![]() ¥¶£¨’€∫€”Î
¥¶£¨’€∫€”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() .
.
£®1£©œfl∂Œ![]() µƒ≥§∂»Œ™__________£ª
µƒ≥§∂»Œ™__________£ª
£®2£©«Û÷±œfl![]() À˘∂‘”¶µƒ∫Ø ˝Ω‚Œˆ Ω£ª
À˘∂‘”¶µƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®3£©»Ùµ„![]() ‘⁄œfl∂Œ
‘⁄œfl∂Œ![]() …œ£¨‘⁄œfl∂Œ
…œ£¨‘⁄œfl∂Œ![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨ πÀƒ±fl–Œ
£¨ πÀƒ±fl–Œ![]() «∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„
«∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡œ¬¡–≤ƒ¡œ£¨ÕÍ≥…»ŒŒÒ£∫
◊‘œ‡À∆Õº–Œ
∂®“£∫»Ùƒ≥∏ˆÕº–Œø…∑÷∏ÓŒ™»Ù∏…∏ˆ∂º”ÎÀ¸œ‡À∆µƒÕº–Œ£¨‘Ú≥∆’‚∏ˆÕº–Œ «◊‘œ‡À∆Õº–Œ£Æ¿˝»Á£∫’˝∑Ω–ŒABCD÷–£¨µ„E°¢F°¢G°¢H∑÷± «AB°¢BC°¢CD°¢DA±flµƒ÷–µ„£¨¡¨Ω”EG£¨HFΩª”⁄µ„O£¨“◊÷™∑÷∏Ó≥…µƒÀƒ∏ˆÀƒ±fl–ŒAEOH°¢EBFO°¢OFCG°¢HOGDæ˘Œ™’˝∑Ω–Œ£¨«“”Α≠’˝∑Ω–Œœ‡À∆£¨π ’˝∑Ω–Œ «◊‘œ‡À∆Õº–Œ£Æ
»ŒŒÒ£∫
£®1£©Õº1÷–’˝∑Ω–ŒABCD∑÷∏Ó≥…µƒÀƒ∏ˆ–°’˝∑Ω–Œ÷–£¨√ø∏ˆ’˝∑Ω–Œ”Α≠’˝∑Ω–Œµƒœ‡À∆±»Œ™°° °°£ª
£®2£©»ÁÕº2£¨“—÷™°˜ABC÷–£¨°œACB=90°„£¨AC=4£¨BC=3£¨–°√˜∑¢œ÷°˜ABC“≤ «°∞◊‘œ‡À∆Õº–Œ°±£¨À˚µƒÀº¬∑ «£∫π˝µ„C◊˜CD°ÕAB”⁄µ„D£¨‘ÚCDΩ´°˜ABC∑÷∏Ó≥…2∏ˆ”ÎÀ¸◊‘º∫œ‡À∆µƒ–°÷±Ω«»˝Ω«–Œ£Æ“—÷™°˜ACD°◊°˜ABC£¨‘Ú°˜ACD”ΰ˜ABCµƒœ‡À∆±»Œ™°° °°£ª
£®3£©œ÷”–“ª∏ˆæÿ–ŒABCD «◊‘œ‡À∆Õº–Œ£¨∆‰÷–≥§AD=a£¨øÌAB=b£®a£æb£©£Æ
«Î¥”œ¬¡–A°¢B¡ΩÂ÷–»Œ—°“ªÃı◊˜¥£∫Œ“—°‘Ò°° °°Ã‚£Æ
A£∫¢Ÿ»ÁÕº3©Å1£¨»ÙΩ´æÿ–ŒABCD◊›œÚ∑÷∏Ó≥…¡Ω∏ˆ»´µ»æÿ–Œ£¨«“”Α≠æÿ–Œ∂ºœ‡À∆£¨‘Úa=°° °°£®”√∫¨bµƒ Ω◊”±Ì 棩£ª
¢⁄»ÁÕº3©Å2»ÙΩ´æÿ–ŒABCD◊›œÚ∑÷∏Ó≥…n∏ˆ»´µ»æÿ–Œ£¨«“”Α≠æÿ–Œ∂ºœ‡À∆£¨‘Úa=°° °°£®”√∫¨n£¨bµƒ Ω◊”±Ì 棩£ª
B£∫¢Ÿ»ÁÕº4©Å1£¨»ÙΩ´æÿ–ŒABCDœ»◊›œÚ∑÷∏Ó≥ˆ2∏ˆ»´µ»æÿ–Œ£¨‘ŸΩ´ £”‡µƒ≤ø∑÷∫·œÚ∑÷∏Ó≥…3∏ˆ»´µ»æÿ–Œ£¨«“∑÷∏Óµ√µΩµƒæÿ–Œ”Α≠æÿ–Œ∂ºœ‡À∆£¨‘Úa=°° °°£®”√∫¨bµƒ Ω◊”±Ì 棩£ª
¢⁄»ÁÕº4©Å2£¨»ÙΩ´æÿ–ŒABCDœ»◊›œÚ∑÷∏Ó≥ˆm∏ˆ»´µ»æÿ–Œ£¨‘ŸΩ´ £”‡µƒ≤ø∑÷∫·œÚ∑÷∏Ó≥…n∏ˆ»´µ»æÿ–Œ£¨«“∑÷∏Óµ√µΩµƒæÿ–Œ”Α≠æÿ–Œ∂ºœ‡À∆£¨‘Úa=°° °°£®”√∫¨m£¨n£¨bµƒ Ω◊”±Ì 棩£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com