
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

���𰸡���1��![]() ����2��
����2��![]() ����3��A����
����3��A����![]() ����
����![]() ��B����
��B����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
�������������������1���������ƱȵĶ�����⼴�ɣ���2���ɹ��ɶ������AB=5���������Ʊȵ���![]() ����ô𰸣���3��A.���ɾ���ABEF����FECD���г�����ʽ�����ɵã�����ÿ��С���ζ���ȫ�ȵģ��ɵ���߳�Ϊb��
����ô𰸣���3��A.���ɾ���ABEF����FECD���г�����ʽ�����ɵã�����ÿ��С���ζ���ȫ�ȵģ��ɵ���߳�Ϊb��![]() a���г�����ʽ�������ɣ�B.�ٷֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ��⣻���������֪����2�����ȫ�ȣ�����3�����Ҳȫ�ȣ�����DN=
a���г�����ʽ�������ɣ�B.�ٷֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ��⣻���������֪����2�����ȫ�ȣ�����3�����Ҳȫ�ȣ�����DN=![]() b��Ȼ��ֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ���.
b��Ȼ��ֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ���.
�⣺��1���ߵ�H��AD���е㣬
��AH=![]() AD��
AD��
��������AEOH��������ABCD��
�����Ʊ�Ϊ��![]() ==
==![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����Rt��ABC�У�AC=4��BC=3�����ݹ��ɶ����ã�AB=5��
���ACD���ABC���Ƶ����Ʊ�Ϊ��![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3��A���١߾���ABEF����FECD��
��AF��AB=AB��AD��
��![]() a��b=b��a��
a��b=b��a��
��a=![]() b��
b��
�ʴ�Ϊ��![]()
��ÿ��С���ζ���ȫ�ȵģ�����߳�Ϊb��![]() a��
a��
��b��![]() a=a��b��
a=a��b��
��a=![]() b��
b��
�ʴ�Ϊ��![]()
B������ͼ2��
�ɢ٢ڿ�֪����2�����ȫ�ȣ�����3�����Ҳȫ�ȣ�
��DN=![]() b��
b��
������FM�Ǿ���DFMN�ij�ʱ��
�߾���FMND����ABCD��
��FD��DN=AD��AB��
��FD��![]() b=a��b��
b=a��b��
���FD=![]() a��
a��
��AF=a��![]() a=
a=![]() a��
a��
��AG=![]() =
=![]() =
=![]() a��
a��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() a��b=b��a
a��b=b��a
�ã�a=![]() b��
b��
������DF�Ǿ���DFMN�ij�ʱ��
�߾���DFMN����ABCD��
��FD��DN=AB��AD
��FD��![]() b=b��a
b=b��a
���FD=![]() ��
��
��AF=a��![]() =
=![]() ��
��
��AG=![]() =
=![]() ��
��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() ��b=b��a��
��b=b��a��
�ã�a=![]() b��
b��
�ʴ�Ϊ��![]() ��
��![]() ��
��
����ͼ3��
�ɢ٢ڿ�֪����m�����ȫ�ȣ�����n�����Ҳȫ�ȣ�
��DN=![]() b��
b��
������FM�Ǿ���DFMN�ij�ʱ��
�߾���FMND����ABCD��
��FD��DN=AD��AB��
��FD��![]() b=a��b��
b=a��b��
���FD=![]() a��
a��
��AF=a��![]() a��
a��
��AG=![]() =
=![]() =
=![]() a��
a��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() a��b=b��a
a��b=b��a
�ã�a=![]() b��
b��
������DF�Ǿ���DFMN�ij�ʱ��
�߾���DFMN����ABCD��
��FD��DN=AB��AD
��FD��![]() b=b��a
b=b��a
���FD=![]() ��
��
��AF=a��![]() ��
��
��AG=![]() =
=![]() ��
��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() ��b=b��a��
��b=b��a��
�ã�a=![]() b��
b��
�ʴ�Ϊ��![]() b��
b��![]() b��
b��




 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����a��0ʱ����![]() ��ֵ����д�������̣�
��ֵ����д�������̣�
��2����a��0��b��0����![]() +
+![]() =0����
=0����![]() ��ֵΪ�� ����
��ֵΪ�� ����
��3����ab��0����![]() +
+![]() +
+![]() ��ֵΪ�� ����
��ֵΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��23���ǡ���������ա���ijУ��ѧ������������˲���ѧ�����͡�����ϲ����ͼ����𡱣�ֻѡһ���ѧ�������Ķ���������˵���ͳ�ƣ���������ͳ�ƺ���Ƴ�����ͳ�Ʊ�������ͳ��ͼ�������ͳ��ͼ���ṩ����Ϣ����������⣺
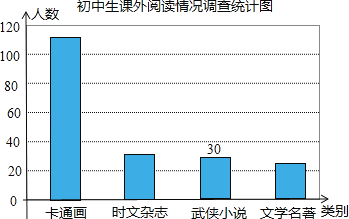
�����������Ķ��������ͳ�Ʊ�
���� | Ƶ�� | Ƶ�� |
��ͨ�� | a | 0.56 |
ʱ����־ | 32 | b |
����С˵ | c | 0.15 |
��ѧ���� | 26 | d |
��1�������������˼���ѧ����ͳ�Ʊ���a��d������ʲô��ֵ��
��2���Թ��Ƹ�У1500��ѧ�����ж�����ͬѧ��ϲ����ѧ�������鼮��
��3���������ͳ�����ݣ�����վ����ѧ���ŵ���������һ����Ŀ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
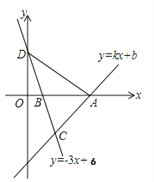
����Ŀ����ͼ,һ�κ���y=kx+b��ͼ����A(8,0)��ֱ��y=-3x+6��x�ύ�ڵ�B,��y�ύ�ڵ�D,����ֱ�߽��ڵ�C(4,m).
(1)��m��ֵ��һ�κ����Ľ���ʽ��
(2)���ACD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У���B����C��AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ�
��1������B��30�㣬��C��50�㣮���DAE�Ķ������� ������ֱ��д���𰸣�
��2��д����DAE����B����C��������ϵ���� ������֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��һ����λ��������a��ʾʮλ�ϵ����֣�b��ʾ��λ�ϵ����֣�a��b��ab��0�����������λ���ö���ʽ��ʾΪ�� ������a��b��ʽ�ӣ�������ʮλ����λ�ϵ����ֻ���λ�õõ�һ������λ��������������λ���ĺ�һ���ܱ��� ����������������λ���IJ�һ���ܱ��� ������.
��2��һ����λ������F��������λ�ϵ����ֻ�����ͬ�Ҷ���Ϊ0���������İ�λ��ʮλ����λ�ϵ�����������ѡ�������������6����ͬ����λ��������6����λ���ĺ͵��������λ�������������������λ��FΪ���Ѻ����������磺132�����Ѻ�����.
һ����λ������P��������λ�ϵ����ֻ�����ͬ�Ҷ���Ϊ0��������ʮλ���ֵ��ڰ�λ�������λ���ֵĺͣ������������λ��PΪ����ƽ������
��ֱ���ж�123�Dz������Ѻ�������
��ֱ��д�������� ��������ƽ������
��ͨ���з��̵ķ��������������ƽ�����������Ѻ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() �������ֱ���
�������ֱ���![]() ��
��![]() ���˶�������
���˶�������![]() ���˶��ٶ���ÿ��2����λ���ȣ����ǵ�
���˶��ٶ���ÿ��2����λ���ȣ����ǵ�![]() �˶��ٶȵ�2����������һ���㵽���յ�ʱ��ֹͣһ���˶�����
�˶��ٶȵ�2����������һ���㵽���յ�ʱ��ֹͣһ���˶�����![]() Ϊ�Գ�����
Ϊ�Գ�����![]() �ĶԳ�ͼ��
�ĶԳ�ͼ��![]() ����
����![]() ǡ����
ǡ����![]() �ϵ�ʱ��Ϊ__�룮�������˶������У�
�ϵ�ʱ��Ϊ__�룮�������˶������У�![]() �����
�����![]() �ص�������������ֵΪ________________��
�ص�������������ֵΪ________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�ֳɱ�Ϊ40Ԫ![]() ǧ�˵���Ʒ,����50Ԫ
ǧ�˵���Ʒ,����50Ԫ![]() ǧ������,һ���¿��۳�500ǧ��,�ִ����Ǽ�����,���г�����,�Ǽ�xԪʱ,��������Ϊmǧ��,m��x��һ�κ���,�����������±���
ǧ������,һ���¿��۳�500ǧ��,�ִ����Ǽ�����,���г�����,�Ǽ�xԪʱ,��������Ϊmǧ��,m��x��һ�κ���,�����������±���

![]() �۲��������,ֱ��д��m��x�ĺ�����ϵʽ��_______________�����Ǽ�5Ԫʱ,����ɵ�������������___________Ԫ��
�۲��������,ֱ��д��m��x�ĺ�����ϵʽ��_______________�����Ǽ�5Ԫʱ,����ɵ�������������___________Ԫ��
![]() ���ۼ۶�����Ԫʱ,���������������������������
���ۼ۶�����Ԫʱ,���������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ���������С�������ᣬ����С������һ����������û���ã�ʹ����������������������ȥ������һ���һ������ѡ���
��1�����С����һ�ⲻʹ��������������ôС����Ե�һ����ĸ�����������
��2�����С���������������ڵڶ���ʹ�ã�������״ͼ�����б�������С��˳��ͨ�صĸ��ʣ�
��3���Ӹ��ʵĽǶȷ������㽨��С���ڵڼ���ʹ��������������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com