
����Ŀ����1��һ����λ��������a��ʾʮλ�ϵ����֣�b��ʾ��λ�ϵ����֣�a��b��ab��0�����������λ���ö���ʽ��ʾΪ�� ������a��b��ʽ�ӣ�������ʮλ����λ�ϵ����ֻ���λ�õõ�һ������λ��������������λ���ĺ�һ���ܱ��� ����������������λ���IJ�һ���ܱ��� ������.
��2��һ����λ������F��������λ�ϵ����ֻ�����ͬ�Ҷ���Ϊ0���������İ�λ��ʮλ����λ�ϵ�����������ѡ�������������6����ͬ����λ��������6����λ���ĺ͵��������λ�������������������λ��FΪ���Ѻ����������磺132�����Ѻ�����.
һ����λ������P��������λ�ϵ����ֻ�����ͬ�Ҷ���Ϊ0��������ʮλ���ֵ��ڰ�λ�������λ���ֵĺͣ������������λ��PΪ����ƽ������
��ֱ���ж�123�Dz������Ѻ�������
��ֱ��д�������� ��������ƽ������
��ͨ���з��̵ķ��������������ƽ�����������Ѻ�����������
���𰸡�(1) 10a+b��11��9��(2) ��123�������Ѻ����������ɼ���������32���ۼ�������ƽ�����������Ѻ�����������396��264��132��
��������
��1���ֱ���������ĺ��������IJ�ɵõ����ۣ�
��2���ٸ������Ѻ������Ķ����жϼ��ɣ�
�ڸ�������ƽ�����Ķ����оٳ����е�����ƽ�������ɣ�
������λ��![]() ��������ƽ�����������Ѻ���������������ƽ�����Ķ��壬�ó�y��x+z���������Ѻ������Ķ��壬�ó�10x+y+10y+x+10x+z+10z+x+10y+z+10z+y��100x+10y+z������Ϊ12y��78x��21z����y��x+z���룬�����ó�z��2x��Ȼ��Ӣڵ���������ѡ������Ҫ���������.
��������ƽ�����������Ѻ���������������ƽ�����Ķ��壬�ó�y��x+z���������Ѻ������Ķ��壬�ó�10x+y+10y+x+10x+z+10z+x+10y+z+10z+y��100x+10y+z������Ϊ12y��78x��21z����y��x+z���룬�����ó�z��2x��Ȼ��Ӣڵ���������ѡ������Ҫ���������.
(1)�����λ���ö���ʽ��ʾΪ10a+b��
��10a+b��+��10b+a����10a+b+10b+a��11a+11b��11��a+b����
��11��a+b����11��a+b����������
�������λ���ĺ�һ���ܱ���11������
��10a+b������10b+a����10a+b��10b��a��9a��9b��9��a��b����
��9��a��b����9��a��b����������
����������λ���IJ�һ���ܱ���9������
�ʴ�Ϊ��11��9��
(2)��123�������Ѻ��������������£�
��12+21+13+31+23+32��132��123��
��123�������Ѻ�������
��ʮλ������9������ƽ������198��297��396��495��594��693��792��891��һ��8����
ʮλ������8������ƽ������187��286��385��584��682��781��һ��6����
ʮλ������7������ƽ������176��275��374��473��572��671��һ��6����
ʮλ������6������ƽ������165��264��462��561��һ��4����
ʮλ������5������ƽ������154��253��352��451��һ��4����
ʮλ������4������ƽ������143��341��һ��2����
ʮλ������3������ƽ������132��231��һ��2����
���ԣ�����ƽ����һ����8+��6+4+2����2��32����
�ʴ�Ϊ32��
������λ��![]() ��������ƽ�����������Ѻ�������
��������ƽ�����������Ѻ�������
����λ��![]() ������ƽ������
������ƽ������
��y��x+z��
��![]() �����Ѻ�������
�����Ѻ�������
��10x+y+10y+x+10x+z+10z+x+10y+z+10z+y��100x+10y+z��
��22x+22y+22z��100x+10y+z��
��12y��78x��21z��
��y��x+z���룬��12x+12z��78x��21z��
��33z��66x��
��z��2x��
�ɢڿ�֪����������ƽ�����������Ѻ�����������396��264��132��


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����µף�ijѧУӭ��������ѧ��ͨʶƷī�ϣ�������������ɽ��Ϊ�����ѧϰ�ڻ.Ϊ����ͬѧ�Ǹ��õ��˽��ʮ�Ľ�����֪ʶ������ѧϰ������Ϯ����������Ŀ�Ļ����ϣ�����������ʮ�Ľ���֮������Ŀ������չ�����֪ʶ����.��ѧУ�ߡ����꼶����400��ѧ���μ�����ξ������ִ��ߡ����꼶�������ȡ20��ѧ���ijɼ����г�������.
�ռ���������:
���꼶:
![]()
���꼶:
![]()
������������:

�����������£�

����������Ϣ���ش���������:
(1)a=______��b=______��
(2)����Ϊ�ĸ��꼶֪ʶ����������ɼ��Ϻã�˵������(���ٴ�������ͬ�ĽǶ�˵���ƶϵĺ�����)��
(3)ѧУ��֪ʶ�����ɼ�������80�ֵ�ѧ���䷢��ʤ�����������ѧУ�ߡ����꼶����ѧ���л����ʤ���Ĵ�Լ��_____��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦԪ�����ڼ䵽������Բ�̳�����һ̨ijƷ�ƱʼDZ����ԣ�ǡ���̳����Ƴ���ӭԪ�����������ۻ�������Ż���������
�����ܽ�ԭ�ۣ� | �ۿ� |
������5000Ԫ�IJ��� | ���� |
����5000Ԫ�Ҳ�����10000Ԫ�IJ��� | ���� |
����10000Ԫ�Ҳ�����20000Ԫ�IJ��� | ���� |
���� | ���� |
���磺���������Ʒԭ��Ϊ15000Ԫ��ʵ�ʸ�����Ϊ��
5000��90%+��10000��5000����80%+��15000��10000����70%��12000Ԫ��
��1��������Ʒ�Ƶ��Ե�ԭ��Ϊ8000Ԫ/̨�����������ʦʵ�ʸ����
��2����֪����ʦ����һ̨��Ʒ�Ƶ���ʵ�ʸ���5700Ԫ��
�����Ʒ�Ƶ��Ե�ԭ���Ƕ���Ԫ/̨��
�����۳���̨�����̳��Կɻ���14%��������Ʒ�Ƶ��ԵĽ���Ϊ����Ԫ/̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=kx2+��k��2��x��2������k��0����
��1�������������x��Ľ��㼰��������꣨�����ú�k�Ĵ���ʽ��ʾ����
��2�����Ǹ������߶��������ΪP��m��n����ֱ��д��|n|����Сֵ��
��3������������������ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���ȣ�����k�ı仯��ƽ�ƺ�������ߵĶ��㶼��ij���º�����ͼ���ϣ����º����Ľ���ʽ����Ҫ��д�Ա�����ȡֵ��Χ����
����λ���ȣ�����k�ı仯��ƽ�ƺ�������ߵĶ��㶼��ij���º�����ͼ���ϣ����º����Ľ���ʽ����Ҫ��д�Ա�����ȡֵ��Χ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() �����Բ��AB��
�����Բ��AB��![]() ��ֱ����D��AB�ӳ��ߵ�һ�㣬
��ֱ����D��AB�ӳ��ߵ�һ�㣬 ![]() ��DC���ӳ�����
��DC���ӳ�����![]()
![]() ��F����
��F����![]() ��
��
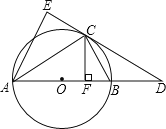
![]() ��֤��DE��
��֤��DE��![]() �����ߣ�
�����ߣ�
![]() ��
��![]() ����AE��BC�ij���
����AE��BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ʦ����������ѧ����ѧϰ״���ֳ�![]() �ĸ��ȼ����Ƴɲ�������ͳ��ͼ��
�ĸ��ȼ����Ƴɲ�������ͳ��ͼ��
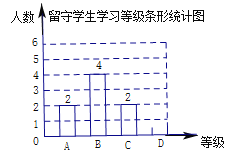
![]()

��1���ð��ж���������ѧ��������������ͳ��ͼ����������
��2����ѧ��ʦ������![]() �ȼ�������ѧ������ѡ����������ѧѧϰ�����ʹ���б�����״ͼ�ķ����������ѡ�������������ѧ������ͬһ�ȼ��ĸ��ʣ�
�ȼ�������ѧ������ѡ����������ѧѧϰ�����ʹ���б�����״ͼ�ķ����������ѡ�������������ѧ������ͬһ�ȼ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx��3��A��1��0����B����3��0����ֱ��AD���������ڵ�D����D�ĺ�����Ϊ��2����P��m��n�����߶�AD�ϵĶ��㣮
��1����ֱ��AD�������ߵĽ���ʽ��
��2������P��ֱ�ߴ�ֱ��x�ᣬ���������ڵ�Q�����߶�PQ�ij���l��m�Ĺ�ϵʽ��mΪ��ֵʱ��PQ���
��3����ƽ�����Ƿ�������㣨�ᡢ�����궼Ϊ������R��ʹ��P��Q��D��RΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����R�����ꣻ�������ڣ�˵�����ɣ�
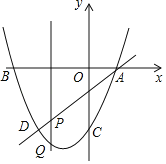
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABCD�У�P�ǶԽ���AC�ϵ�һ�㣬��E��BC���ӳ����ϣ���PE=PB��
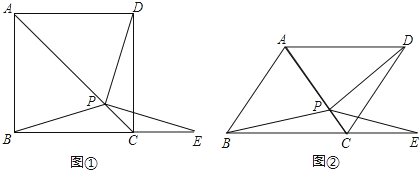
��1����֤����BCP�ա�DCP��
��2����֤����DPE=��ABC��
��3����������ABCD��Ϊ���Σ������������䣨��ͼ����������ABC=58�㣬����DPE=�� ���ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com