
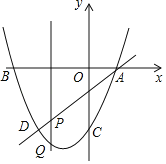
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
【答案】(1)y=x2+2x﹣3;(2)当m=-![]() 时,PQ最长,最大值为
时,PQ最长,最大值为![]() ;(3)R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3).
;(3)R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3).
【解析】
(1)根据待定系数法,可得抛物线的解析式;根据自变量与函数值的对应关系,可得D点坐标,再根据待定系数法,可得直线的解析式;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
(3)根据PQ的长是正整数,可得PQ,根据平行四边形的性质,对边平行且相等,可得DR的长,根据点的坐标表示方法,可得答案
解:(1)将A(1,0),B(﹣3,0)代入y=ax2+bx﹣3得:
![]() 解得:
解得:![]()
∴抛物线的解析式为:y=x2+2x﹣3,
当x=﹣2时,y=(﹣2)2﹣4﹣3=﹣3,
∴D(﹣2,﹣3),
设直线AD的解析式为y=kx+b,将A(1,0),D(﹣2,﹣3)代入得:
![]() 解得:
解得:![]()
∴直线AD的解析式为y=x﹣1;
因此直线AD的解析式为y=x﹣1,抛物线的解析式为:y=x2+2x﹣3.
(2)∵点P在直线AD上,Q抛物线上,P(m,n),
∴n=m﹣1 Q(m,m2+2m﹣3)
∴PQ的长l=(m﹣1)﹣(m2+2m﹣3)=﹣m2﹣m+2 (﹣2≤m≤1)
∴当m=![]() 时,PQ的长l最大=﹣(
时,PQ的长l最大=﹣(![]() )2﹣(
)2﹣(![]() )+2=
)+2=![]() .
.
答:线段PQ的长度l与m的关系式为:l=﹣m2﹣m+2 (﹣2≤m≤1)
当m=![]() 时,PQ最长,最大值为
时,PQ最长,最大值为![]() .
.
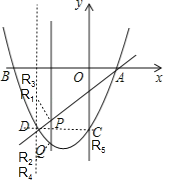
(3)①若PQ为平行四边形的一边,则R一定在直线x=﹣2上,如图:
∵PQ的长为0<PQ≤![]() 的整数,
的整数,
∴PQ=1或PQ=2,
当PQ=1时,则DR=1,此时,在点D上方有R1(﹣2,﹣2),在点D下方有R2(﹣2,﹣4);
当PQ=2时,则DR=2,此时,在点D上方有R3(﹣2,﹣1),在点D下方有R4(﹣2,﹣5);
②若PQ为平行四边形的一条对角线,则PQ与DR互相平分,此时R与点C重合,即R5(0,﹣3)
综上所述,符合条件的点R有:R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3).
答:符合条件的点R共有5个,即:R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3).


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算:(-![]() )÷(
)÷(![]()
![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]()
![]() )÷(
)÷(![]() )=(
)=(![]()
![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]()
![]() )=
)=![]() .
.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-![]() )÷(
)÷(![]()
![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位正整数,a表示十位上的数字,b表示个位上的数字(a≠b,ab≠0),则这个两位数用多项式表示为 (含a、b的式子);若把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被 整除,这两个两位数的差一定能被 整除.
(2)一个三位正整数F,各个数位上的数字互不相同且都不为0.若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数.若这6个两位数的和等于这个三位数本身,则称这样的三位数F为“友好数”,例如:132是“友好数”.
一个三位正整数P,各个数位上的数字互不相同且都不为0,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数P为“和平数”;
①直接判断123是不是“友好数”?
②直接写出共有 个“和平数”;
③通过列方程的方法求出既是“和平数”又是“友好数”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知PA=PB=PC=2,∠BPC=120°,PA∥BC.以AB、PB为边作平行四边形ABPD,连接CD,则CD的长为( )

A. 2![]() B. 2
B. 2![]() C.
C. ![]() +1D.
+1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为40元![]() 千克的商品,若按50元
千克的商品,若按50元![]() 千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:
千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:

![]() 观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
![]() 当售价定多少元时,会获得月销售最大利润,求出最大利润.
当售价定多少元时,会获得月销售最大利润,求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推广“阳光体育”大课间活动,高新中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
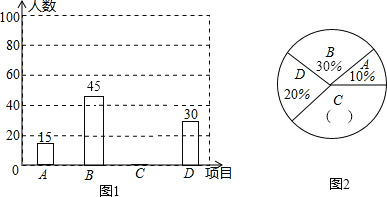
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=-2x+4,下列结论错误的是( )
A. 函数的图象与x轴的交点坐标是![]()
B. 函数值随自变量的增大而减小
C. 函数的图象不经过第三象限
D. 函数的图象向下平移4个单位长度得![]() 的图象
的图象
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com