
【题目】数学老师布置了一道思考题“计算:(-![]() )÷(
)÷(![]()
![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]()
![]() )÷(
)÷(![]() )=(
)=(![]()
![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]()
![]() )=
)=![]() .
.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-![]() )÷(
)÷(![]()
![]() +
+![]() ).
).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】计算:(直接写结果)
(1)- 5+ 2 =
(2)-5-2=
(3)5-(-2)=
(4)(-5)×(-2)=
(5)(-2)÷(-6)=
(6)![]() =
=
(7)![]() =
=
(8)![]() =
=
(9)![]() =
=
(10)![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了“二十四节气之旅”项目,并开展了相关知识竞赛.该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查.
收集数据如下:
七年级:
![]()
八年级:
![]()
整理数据如下:

分析数据如下:

根据以上信息,回答下列问题:
(1)a=______,b=______;
(2)你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性);
(3)学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3∥…,则正方形A2018B2018C2018D2018的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b满足![]() ,
,![]() ,且有理数a、b、c在数轴上对应的点分别为A、B、C.
,且有理数a、b、c在数轴上对应的点分别为A、B、C.
![]() 则
则![]() ______,
______,![]() ______,
______,![]() ______.
______.
![]() 点D是数轴上A点右侧一动点,点E、点F分别为CD、AD中点,当点D运动时,线段EF的长度是否发生变化,若变化,请说明理由,若不变,请求出其值;
点D是数轴上A点右侧一动点,点E、点F分别为CD、AD中点,当点D运动时,线段EF的长度是否发生变化,若变化,请说明理由,若不变,请求出其值;
![]() 若点A、B、C在数轴上运动,其中点C以每秒1个单位的速度向左运动,同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动
若点A、B、C在数轴上运动,其中点C以每秒1个单位的速度向左运动,同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动![]() 请问:是否存在一个常数m使得
请问:是否存在一个常数m使得![]() 不随运动时间t的改变而改变
不随运动时间t的改变而改变![]() 若存在,请求出m和这个不变化的值;若不存在,请说明理由.
若存在,请求出m和这个不变化的值;若不存在,请说明理由.
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师元旦节期间到武商众圆商场购买一台某品牌笔记本电脑,恰逢商场正推出“迎元旦”促销打折活动,具体优惠情况如表:
购物总金额(原价) | 折扣 |
不超过5000元的部分 | 九折 |
超过5000元且不超过10000元的部分 | 八折 |
超过10000元且不超过20000元的部分 | 七折 |
…… | …… |
例如:若购买的商品原价为15000元,实际付款金额为:
5000×90%+(10000﹣5000)×80%+(15000﹣10000)×70%=12000元.
(1)若这种品牌电脑的原价为8000元/台,请求出张老师实际付款金额;
(2)已知张老师购买一台该品牌电脑实际付费5700元.
①求该品牌电脑的原价是多少元/台?
②若售出这台电脑商场仍可获利14%,求这种品牌电脑的进价为多少元/台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=kx2+(k﹣2)x﹣2(其中k>0).
(1)求该抛物线与x轴的交点及顶点的坐标(可以用含k的代数式表示);
(2)若记该抛物线顶点的坐标为P(m,n),直接写出|n|的最小值;
(3)将该抛物线先向右平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
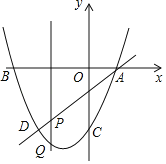
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com