
【题目】已知抛物线y=kx2+(k﹣2)x﹣2(其中k>0).
(1)求该抛物线与x轴的交点及顶点的坐标(可以用含k的代数式表示);
(2)若记该抛物线顶点的坐标为P(m,n),直接写出|n|的最小值;
(3)将该抛物线先向右平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
【答案】(1)抛物线的顶点坐标是(![]() ,﹣
,﹣![]() );(2)当k=2时,|n|的最小值是2;(3)新函数的解析式为y=﹣
);(2)当k=2时,|n|的最小值是2;(3)新函数的解析式为y=﹣![]() ﹣1.
﹣1.
【解析】试题分析:(1)令y=0,解方程kx2+(k﹣2)x﹣2=0即可得到抛物线与x轴的交点,根据抛物线的顶点坐标公式(﹣![]() )代入进行计算即可求解;
)代入进行计算即可求解;
(2)根据(1)的结果,然后利用绝对值的性质,再根据不等式的性质进行解答;
(3)根据左加右减,上加下减,写出平移后的抛物线顶点坐标,然后消掉字母k即可得解.
试题解析:解:(1)当y=0时,kx2+(k﹣2)x﹣2=0,即(kx﹣2)(x+1)=0,解得:x1=![]() ,x2=﹣1,∴抛物线与x轴的交点坐标是(
,x2=﹣1,∴抛物线与x轴的交点坐标是(![]() ,0)与(﹣1,0),﹣
,0)与(﹣1,0),﹣![]() =﹣
=﹣![]() =
=![]() ﹣
﹣![]() =
=![]() =﹣
=﹣![]() ,∴抛物线的顶点坐标是(
,∴抛物线的顶点坐标是(![]() ﹣
﹣![]() ,﹣
,﹣![]() );
);
(2)根据(1),|n|=|﹣![]() |=
|=![]() =
=![]() =
=![]() +
+![]() +1≥2
+1≥2![]() +1=1+1=2,当且仅当
+1=1+1=2,当且仅当![]() =
=![]() ,即k=2时取等号,∴当k=2时,|n|的最小值是2;
,即k=2时取等号,∴当k=2时,|n|的最小值是2;
(3)![]() ﹣
﹣![]() +
+![]() =
=![]() ,﹣
,﹣![]() +
+![]() =
=![]() =
=![]() =﹣
=﹣![]() k﹣1,设平移后的抛物线的顶点坐标为(x,y),则
k﹣1,设平移后的抛物线的顶点坐标为(x,y),则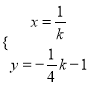 ,消掉字母k得:y=﹣
,消掉字母k得:y=﹣![]() ﹣1,∴新函数的解析式为y=﹣
﹣1,∴新函数的解析式为y=﹣![]() ﹣1.
﹣1.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】小东和小明要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边CD上有水池及建筑遮挡,没有办法直接测量其长度.
小东经测量得知AB=AD=5m,∠A=60°,BC=12m,∠ABC=150°.
小明说根据小东所得的数据可以求出CD的长度.
你同意小明的说法吗?若同意,请求出CD的长度;若不同意,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算:(-![]() )÷(
)÷(![]()
![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]()
![]() )÷(
)÷(![]() )=(
)=(![]()
![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]()
![]() )=
)=![]() .
.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-![]() )÷(
)÷(![]()
![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
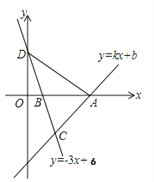
【题目】如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).
(1)求m的值及一次函数的解析式;
(2)求△ACD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
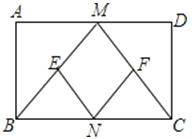
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位正整数,a表示十位上的数字,b表示个位上的数字(a≠b,ab≠0),则这个两位数用多项式表示为 (含a、b的式子);若把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被 整除,这两个两位数的差一定能被 整除.
(2)一个三位正整数F,各个数位上的数字互不相同且都不为0.若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数.若这6个两位数的和等于这个三位数本身,则称这样的三位数F为“友好数”,例如:132是“友好数”.
一个三位正整数P,各个数位上的数字互不相同且都不为0,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数P为“和平数”;
①直接判断123是不是“友好数”?
②直接写出共有 个“和平数”;
③通过列方程的方法求出既是“和平数”又是“友好数”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知PA=PB=PC=2,∠BPC=120°,PA∥BC.以AB、PB为边作平行四边形ABPD,连接CD,则CD的长为( )

A. 2![]() B. 2
B. 2![]() C.
C. ![]() +1D.
+1D. ![]() ﹣1
﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com