
����Ŀ�����ɶ������ض��������֤�����������еġ������������������У�����ϲ�ط��֣�������ȫ�ȵ�ֱ����������ͼ��1���ڷ�ʱ�����������������֤�����ɶ�������������
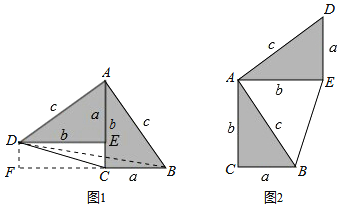
��ͼ��1����DAB=90�㣬��֤��a2+b2=c2
֤��������DB������D��DF��BC��BC���ӳ����ڵ�F����DF=b-a
S�ı���ADCB=![]()
S�ı���ADCB=![]()
��![]() ����ã�a2+b2=c2
����ã�a2+b2=c2
���������֤�������á�������������ͼ��2���Ĺ��ɶ�����֤������ͼ��2���С�DAB=90�㣬��֤��a2+b2=c2

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
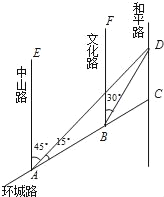
����Ŀ����ͼ��AC��ij�л���·��һ�Σ�AE��BF��CD�����ϱ�����Ľֵ������뻷��·AC�Ľ���·�ڷֱ���A��B��C����������������Dλ�ڵ�A�ı�ƫ��45������B�ı�ƫ��30�������ϣ�AB=2km����DAC=15�㣮
��1����B��D֮��ľ��룻
��2����C��D֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D����O������DF����AC�ڵ�F��
��1����֤��DF��AC��
��2������O�İ뾶Ϊ4����CDF��22.5��������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬����
Ϊ����ԭ�㣬����![]() �Ķ���
�Ķ���![]() ��
��![]() ��������
��������![]() ��һ����
��һ����![]() ��ֱ��
��ֱ��![]() �۵���ʹ�õ�
�۵���ʹ�õ�![]() ���ڶԽ���
���ڶԽ���![]() �ϵĵ�
�ϵĵ�![]() �����ۺ���
�����ۺ���![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
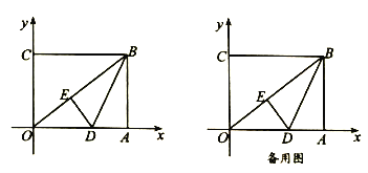
��1���߶�![]() �ij���Ϊ__________��
�ij���Ϊ__________��
��2����ֱ��![]() ����Ӧ�ĺ�������ʽ��
����Ӧ�ĺ�������ʽ��
��3������![]() ���߶�
���߶�![]() �ϣ����߶�
�ϣ����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ�ı���
��ʹ�ı���![]() ��ƽ���ı��Σ������ڣ��������
��ƽ���ı��Σ������ڣ��������![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ķ�ͼ����ƿ̻���������֮��Ĺ�ϵ���밴ͼ��˳�����������龰��֮��Ӧ������������.
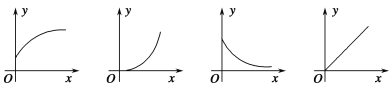
��һ�������ڹ�·��������ʻ��������ʻ��·����ʱ��Ĺ�ϵ��
������ƿ������עˮ��ˮ��ĸ߶���עˮʱ��Ĺ�ϵ��
���������µ��¶ȼƲ���һ����ˮ�У��¶ȼƵĶ�����ʱ��Ĺ�ϵ��
��һ��Խ��Խ����ˮ��ˮ����ʱ��Ĺ�ϵ��
A.�٢ڢܢ� B.�ۢܢڢ�
C.�٢ܢڢ� D.�ۢڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ���ر������������(����ͼ)�������Ϲ����������ĵ���֮������7,�����ķ�ͼ�п����۳ɷ��Ϲ�������ӵ����� ��
![]()
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
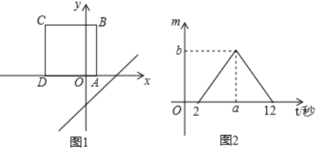
����Ŀ����ͼ1����������ABCD����ƽ��ֱ������ϵ�У�����AD����x���ϣ�������߾���������ƽ�У�ֱ��l��y��x��3��x��ĸ�������ÿ��1����λ���ٶ�ƽ�ƣ���ƽ�ƵĹ����У���ֱ�߱�������ABCD�ı����صõ��߶γ�Ϊm��ƽ�Ƶ�ʱ��Ϊt���룩��m��t�ĺ���ͼ����ͼ2��ʾ����ͼ2��b��ֵΪ�� ��
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() ��ֱƽ��
��ֱƽ��![]() ���ֱ�
���ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ��ֱƽ��
��ֱƽ��![]() ���ֱ�
���ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
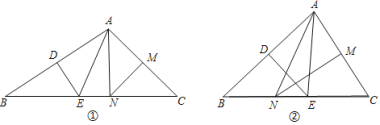
����ͼ�٣���![]() ����
����![]() �Ķ�����
�Ķ�����
����ͼ�ڣ���![]() ����
����![]() �Ķ�����
�Ķ�����
����![]()
![]() ��ֱ��д����
��ֱ��д����![]() ��ʾ
��ʾ![]() ��С�Ĵ���ʽ��
��С�Ĵ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com