
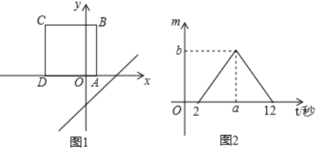
【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
【答案】A
【解析】
根据题意可分析出当t=2时,l经过点A,从而求出OA的长,l经过点C时,t=12,从而可求出a,由a的值可求出AD的长,再根据等腰直角三角形的性质可求出BD的长,即b的值.
解:连接BD,如图所示:
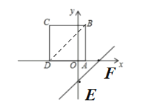
直线y=x﹣3中,令y=0,得x=3;令x=0,得y=﹣3,
即直线y=x﹣3与坐标轴围成的△OEF为等腰直角三角形,
∴直线l与直线BD平行,即直线l沿x轴的负方向平移时,同时经过B,D两点,
由图2可得,t=2时,直线l经过点A,
∴AO=3﹣2×1=1,
∴A(1,0),
由图2可得,t=12时,直线l经过点C,
∴当t=![]() +2=7时,直线l经过B,D两点,
+2=7时,直线l经过B,D两点,
∴AD=(7﹣2)×1=5,
∴在等腰Rt△ABD中,BD=![]() ,
,
即当a=7时,b=![]() .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点对应的有理数分别为a和b,且a和b满足|a+4|+(2b﹣12)2=0.
![]()
(1)求a,b的值;
(2)点C是数轴上一点,其对应的数是x.
①若点C在点A,B之间,化简|x+4|﹣|x﹣6|;
②若CB=2CA,求x的值;
(3)点M和点N分别同时从点O和点A出发,分别以每秒2个单位长度,每秒3个单位长度的速度向数轴正方向运动,与此同时,点T以每秒5个单位长度的速度从点B出发,开始向左运动,遇到点M后立即返回向右运动,遇到点N后立即返回向左运动,与点M相遇后再立即返回,如此往返,直到M、N两点相遇时,点T停止运动,求点T运动的路程一共是多少个单位长度?点T停止的位置所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江夏区某出租车在某一天以江夏体育馆为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9,-2,-5,-4,-12,+8,+3,-1,-4,+10
(1)将最后一名乘客送到目的地,出租车离江夏体育馆出发点多远?
(2)直接写出该出租车在行驶过程中,离江夏体育馆最远的距离是______.
(3)出租车按物价部门规定,行程不超过3km的(含3km),按起步价8元收费,若行程超过3km的,则超过的部分,每千米加收1.2元,该司机这天的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂加工某种茶叶,计划一周生产![]() 千克,平均每天生产
千克,平均每天生产![]() 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?
(![]() )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克![]() 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克![]() 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少![]() 千克扣除
千克扣除![]() 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
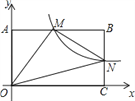
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–![]() x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com