
����Ŀ����ͼ��������A��B�����Ӧ���������ֱ�Ϊa��b����a��b����|a+4|+��2b��12��2��0��
![]()
��1����a��b��ֵ��
��2����C��������һ�㣬���Ӧ������x��
������C�ڵ�A��B֮�䣬����|x+4|��|x��6|��
����CB��2CA����x��ֵ��
��3����M�͵�N�ֱ�ͬʱ�ӵ�O�͵�A�������ֱ���ÿ��2����λ���ȣ�ÿ��3����λ���ȵ��ٶ��������������˶������ͬʱ����T��ÿ��5����λ���ȵ��ٶȴӵ�B��������ʼ�����˶���������M���������������˶���������N���������������˶������M���������������أ����������ֱ��M��N��������ʱ����Tֹͣ�˶������T�˶���·��һ���Ƕ��ٸ���λ���ȣ���Tֹͣ��λ������Ӧ�����Ƕ��٣�
���𰸡���1��a����4��b��6����2����2x��2����x����14����3��20��8.
��������
��1�����ݷǸ��������ʿ����a��b��ֵ��
��2�����ɣ�1���ó�x��ȡֵ��Χ���ٸ��ݾ���ֵ�����ʽ��л�����㣻��������֪����C�������ڵ�B���Ҳ࣬�ֱ�����C��AB֮���C��A���ʱ���з�����⣻
��3����M��N��������ʱ�˶�ʱ��Ϊt�룬��������ʱ����ٶȲ�=��ʼ���룬�г����̿��������ʱ�䣬����T���˶��ٶȳ���ʱ��õ�·�̣�����M��N��T��ͬһ�㣬���M��λ������Ӧ�ĵ�������.
�⣺��1����|a+4|+��2b��12��2��0��
��a+4��0��2b��12��0��
��a����4��b��6��
��2���١ߵ�C�ڵ�A��B֮�䣬
�ੁ4��x��6��
��x+4��0��x��6��0��
|x+4|��|x��6|��x+4����6��x����2x��2��
��������֪����C�������ڵ�B���Ҳ࣬
��BC�ij���Ϊ6��x��AC��|x+4|��
��x����4ʱ��6��x��2��x+4����
��ã�x����![]() ��
��
��x����4ʱ��6��x��2����4��x����
��ã�x����14��
��3����M��N��������ʱ�˶�ʱ��Ϊt�룬
��3t��2t��4��
��t��4��
��T�˶���·��Ϊ��4��5��20��
��ʱM��N��T��ͬһ�㣬
���T��λ������Ӧ����Ϊ��2��4��8��


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д� �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=ax+b��ͼ����㣨��2��1���������������y=ax2��bx+3����������������������ȷ�����ĸ����ǣ�������
�ٹ��㣨2��1�����ڶԳ��������x=1���۵�a��0ʱ���䶥������������СֵΪ3��
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
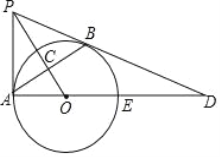
����Ŀ����ͼ��PB���O�����ڵ�B������B��OP�Ĵ���BA������ΪC������O�ڵ�A������PA��AO��AO���ӳ��߽���O�ڵ�E����PB���ӳ��߽��ڵ�D��
��1����֤��PA�ǡ�O�����ߣ�
��2����tan��BAD=![]() ����OC=4����BD�ij���
����OC=4����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ�������һ��С�����ڼ䣬ijѧУ��ίҪ��ѧ���μ�һ�������������꼶ѧ��С�����˽�������ס��С��500������ļ�ͥ���������������������˱�С��һ�����������ͥ���������������ȡ��������λ��Ԫ����������������ݻ��Ƴ�����ֱ��ͼ������ͼ������ͼ���ṩ����Ϣ������������⣺
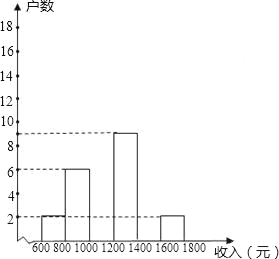
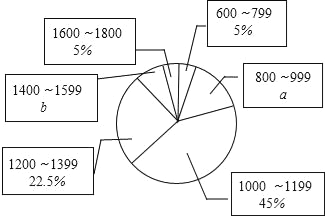
��1����ι��������� ������ͥ�����룬a=�� ����b=�� ����
��2����ȫƵ���ֲ�ֱ��ͼ����������λ�����ڵ��� ����С�飻
��3��������Ƹþ���С����ͥ����ϵͣ�����1000Ԫ���Ļ�����Լ�ж��ٻ���
��4���ڵ�1��͵�5��ļ�ͥ�У������ȡ2����ͥ������������ͥ�˾������������200Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������λ���ĸ�λ������a��ʮλ���ֱȸ�λ���ִ�2��
��1����ʽ��ʾ�����λ����
��2���������λ����ʮλ�ϵ��������λ�ϵ����ֽ���λ�õõ�һ���µ���λ������˵��������ԭ���ĺ��ܱ�22������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P��x��y��������Q������Ϊ��ax+y��x+ay��������aΪ��������Ƶ�Q�ǵ�P����a���������������磬��P��1��4������3����������ΪQ��3��1+4��1+3��4������Q��7��13����
��1����֪��A����2��6������![]() �����������ǵ�A1����B����2������������B1��3��3�������A1�͵�B�����ꣻ
�����������ǵ�A1����B����2������������B1��3��3�������A1�͵�B�����ꣻ
��2����֪��M��m��1��2m��������3����������M��λ��y���ϣ���M�������ꣻ
��3����֪��C����1��3����D��4��3������N��x��y����������n����������N����λ���߶�CD�ϣ���ֱ��д��n��ȡֵ��Χ��
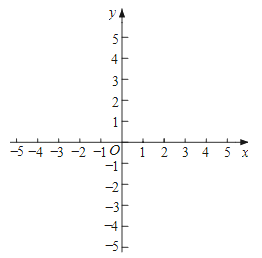
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������9��������������ں���ʡ��ɳ�п�Ļ�����������������������Լδ����.�����㡢����Ĺ����ǻ۵������������������������������й��ٶȣ����й�������Ϊ������Ŀ.��������������һ������������4700���ڴΣ�������˹����������㣬�൱��60������һ�꣬��1��Ϳ������.��4700�����ÿ�ѧ��������ʾΪ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǰϦ��С���������������ɸ����Ӻ���Ѽ����ÿ�����ӵļ۸���ͬ��ÿ����Ѽ���ļ۸���ͬ������֪ij�������ӵļ۸����Ѽ���ļ۸��1.8Ԫ��С�����跢�֣���30Ԫ�������ӵĸ����뻨12Ԫ�������Ѽ��������ͬ��
��1����ó�����������Ѽ���ļ۸���Ƕ���Ԫ��
��2��С������ƻ�������������Ѽ����18��������һ�Ź��│�ϻ������40Ԫ����ֻ�����Ź��│��������ܹ������Ӷ��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD����ƽ��ֱ������ϵ�У�����AD����x���ϣ�������߾���������ƽ�У�ֱ��l��y��x��3��x��ĸ�������ÿ��1����λ���ٶ�ƽ�ƣ���ƽ�ƵĹ����У���ֱ�߱�������ABCD�ı����صõ��߶γ�Ϊm��ƽ�Ƶ�ʱ��Ϊt���룩��m��t�ĺ���ͼ����ͼ2��ʾ����ͼ2��b��ֵΪ�� ��
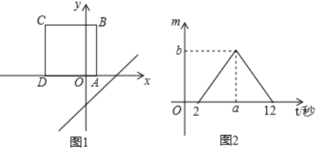
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com