
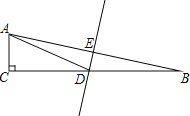
【题目】如图,在直角![]() 中,已知
中,已知![]() ,
,![]() 边的垂直平分线交
边的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长是________.
的长是________.
科目:初中数学 来源: 题型:
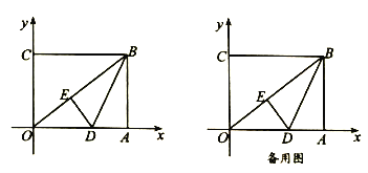
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某文化旅游公司为了在军运会期间更好地宣传武汉,在工厂定制了一批具有浓郁的武汉特色的商品.为了了解市场情况,该公司向市场投放![]() ,
,![]() 型商品共
型商品共![]() 件进行试销,
件进行试销,![]() 型商品成本价
型商品成本价![]() 元/件,
元/件,![]() 商品成本价
商品成本价![]() 元/件,其中
元/件,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型的件数,且不小于
型的件数,且不小于![]() 件,已知
件,已知![]() 型商品的售价为
型商品的售价为![]() 元/件,
元/件,![]() 型商品的售价为
型商品的售价为![]() 元/件,且全部售出.设投放
元/件,且全部售出.设投放![]() 型商品
型商品![]() 件,该公司销售这批商品的利润
件,该公司销售这批商品的利润![]() 元.
元.
(1)直接写出![]() 与
与![]() 之间的函数关系式:_______;
之间的函数关系式:_______;
(2)为了使这批商品的利润最大,该公司应该向市场投放多少件![]() 型商品?最大利润是多少?
型商品?最大利润是多少?
(3)该公司决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元,当该公司售完这
元,当该公司售完这![]() 件商品并捐献资金后获得的最大收益为
件商品并捐献资金后获得的最大收益为![]() 元时,求
元时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为![]() ,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内有四个点A、B、C、D.
(1)请按要求作出图形(注:此题作图不需要写出画法和结论);
①作射线AC;
②作直线BD,交射线AC相于点O;
③分别连接AB、AD;
④求作一条线段MN,使其等于AC﹣AB(用尺规作图,保留作图痕迹).
(2)观察B、D两点间的连线,我们容易判断出线段AB+AD>BD,理由是 ;
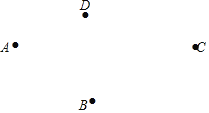
查看答案和解析>>
科目:初中数学 来源: 题型:
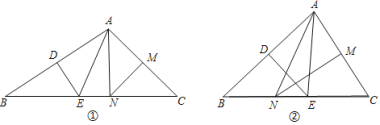
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
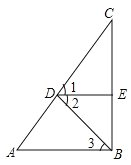
证明:∵ DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°( )
∴DE∥AB(_________ ___)
∴∠2=____ (__________ ___________)
∠1= (____________ _________)
又∵∠1=∠2(_____________________)
∴∠A=∠3(_____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
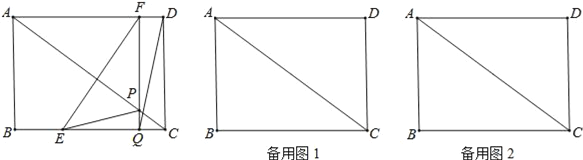
【题目】如图,在矩形ABCD中,AB=6cm,BC=8cm.如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为2cm/s和1cm/s.FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t(s)(0<t<4).
(1)连结EF、DQ,若四边形EQDF为平行四边形,求t的值;
(2)连结EP,设△EPC的面积为ycm2,求y与t的函数关系式,并求y的最大值;
(3)若△EPQ与△ADC相似,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com