
����Ŀ���人ij�Ļ����ι�˾Ϊ���ھ��˻��ڼ���õ������人���ڹ���������һ������Ũ�����人��ɫ����Ʒ��Ϊ���˽��г�������ù�˾���г�Ͷ��![]() ��
��![]() ����Ʒ��
����Ʒ��![]() ������������
������������![]() ����Ʒ�ɱ���
����Ʒ�ɱ���![]() Ԫ/����
Ԫ/����![]() ��Ʒ�ɱ���
��Ʒ�ɱ���![]() Ԫ/��������
Ԫ/��������![]() ����Ʒ�ļ���������
����Ʒ�ļ���������![]() �͵ļ������Ҳ�С��
�͵ļ������Ҳ�С��![]() ������֪
������֪![]() ����Ʒ���ۼ�Ϊ
����Ʒ���ۼ�Ϊ![]() Ԫ������
Ԫ������![]() ����Ʒ���ۼ�Ϊ
����Ʒ���ۼ�Ϊ![]() Ԫ��������ȫ���۳�����Ͷ��
Ԫ��������ȫ���۳�����Ͷ��![]() ����Ʒ
����Ʒ![]() �����ù�˾����������Ʒ������
�����ù�˾����������Ʒ������![]() Ԫ��
Ԫ��
��1��ֱ��д��![]() ��
��![]() ֮��ĺ�����ϵʽ��_______��
֮��ĺ�����ϵʽ��_______��
��2��Ϊ��ʹ������Ʒ��������ù�˾Ӧ�����г�Ͷ�Ŷ��ټ�![]() ����Ʒ����������Ƕ��٣�
����Ʒ����������Ƕ��٣�
��3���ù�˾�������������ÿ�۳�һ��![]() ����Ʒ���ʹ�һ��
����Ʒ���ʹ�һ��![]() ����Ʒ�������о��״����ʽ�
����Ʒ�������о��״����ʽ�![]() Ԫ�����ù�˾������
Ԫ�����ù�˾������![]() ����Ʒ�������ʽ���õ��������Ϊ
����Ʒ�������ʽ���õ��������Ϊ![]() Ԫʱ����
Ԫʱ����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ����2��ӦͶ��
����2��ӦͶ��![]() ��
��![]() ���������Ϊ
���������Ϊ![]() Ԫ����3����������ʱ
Ԫ����3����������ʱ![]() ��ֵΪ
��ֵΪ![]()
��������
��1����������=���ۼ�-�ɱ���![]() �����������
�����������![]() ��
��![]() ֮��ĺ�����ϵʽ.
֮��ĺ�����ϵʽ.
��2��y��![]() ֮����һ�κ�����ϵʽ������һ�κ��������ʿ�֪��x=125ʱy�����ֵ��
֮����һ�κ�����ϵʽ������һ�κ��������ʿ�֪��x=125ʱy�����ֵ��
��3�������ʽ���õ�����Ϊ![]()
![]() ����
����![]() ʱ
ʱ![]() ʱ
ʱ![]() �����ֵ18000���������aֵ.
�����ֵ18000���������aֵ.
��1��![]()
��2���������֪![]() ����
����![]()
��һ�κ��������ʿ�֪��![]() Խ��
Խ��![]() Խ��
Խ��
��![]() ʱ
ʱ ![]()
��ӦͶ��![]() ��
��![]() ���������Ϊ
���������Ϊ![]() Ԫ��
Ԫ��
��3��һ�����![]() Ԫ
Ԫ
��![]()
![]()
�൱![]() ʱ
ʱ![]() ���ֵС��
���ֵС��![]()
��![]() ʱ
ʱ![]() ʱ
ʱ![]() �����ֵ��
�����ֵ��
��![]()
��![]()
����������ʱ![]() ��ֵΪ
��ֵΪ![]() .
.


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������һ���µĽ��ܲ�Ʒ���ò�Ʒ�ijɱ���Ϊ6Ԫ/�����ò�Ʒ����ʽͶ���г�ǰͨ�������������Ϊ��һ����(30��)�������ۣ��ۼ�Ϊ10Ԫ/����������Ա��������������˸��ټ�¼��������¼������Ƴ�ͼ��ͼ�е�����ABC��ʾ��������y(��)������ʱ��x(��)֮��ĺ�����ϵ��
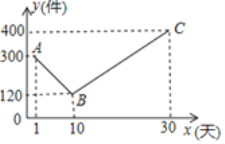
(1)��y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
(2)���ý��ܲ�Ʒ������������ΪW(Ԫ)����W��x֮��ĺ�������ʽ�������������������1040Ԫ���������ж����죿
(3)��5��x��17��ֱ��д���ڼ�������������������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1�Ľ���ʽΪy=��x+2��l1��x�ύ�ڵ�B��ֱ��l2������D��0��5������ֱ��l1���ڵ�C����1��m��������x�ύ�ڵ�A,
��1�����C�����꼰ֱ��l2�Ľ���ʽ��
��2������ABC�������
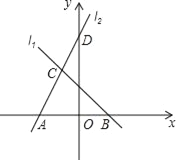
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˺����л���ͳ�Ļ����˽�ѧ�������Ķ���������֯ȫУ��1000��ѧ������һ���Ķ�������������г�ȡ����ѧ���ijɼ�����ͳ�Ʒ��������ݲ��Գɼ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
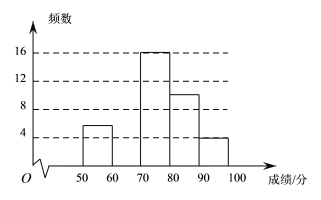
����/�� | Ƶ�� | Ƶ�� |
50��x��60 | 6 | 0.12 |
60��x��70 |
| 0.28 |
70��x��80 | 16 | 0.32 |
80��x��90 | 10 | 0.20 |
90��x��100 | 4 | 0.08 |
��1��Ƶ���ֲ����е�![]() ��
��
��2���������Ƶ���ֲ�ֱ��ͼ����������
��3������ɼ��ﵽ90��90��������Ϊ���㣬���Ƽ��μӾ��������Ƹ�У���������ѧ����Լ�� �ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߶�OB�Ƶ�O��ʱ����ת60���õ��߶�OC��������ת����0�㣼����120�����õ��߶�OD������CD��
��1����ͼ������BD�����BDC�Ĵ�С=_____���ȣ���
��2�����߶�OB����ƽ��ֱ������ϵ�У�O������ԭ�㣬��B������Ϊ����6��0������OBΪб����Rt��OBE��ʹ��OBE=��OCD���ҵ�E�ڵ������ޣ�����CED=90���������Ĵ�С=_____���ȣ�����D������Ϊ_____��
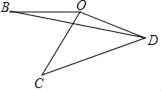
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪ʶ������Ϊ�������ģ�����Ӧ�ð���������������ķ��森����������龰�����������У�
�龰һ���ӽ��ҵ�ͼ��ݣ���������ͬѧ�������е����ᴩ��ƺ������Ϊʲô�أ�������ѧ��ѧ֪ʶ��˵��������⣮

�龰����A��B�Ǻ���l���Ե�������ׯ����Ҫ�ںӱ���һ����ˮվ�����幩ˮ���ʳ�ˮվ����ʲô�ط�����ʹ����Ĺܵ���̣�����ͼ�б�ʾ����ˮվ��P��λ�ã���˵��������ɣ�

����ͬ������������������ΪӦ����ѧ֪ʶΪ�������ʱӦע��ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
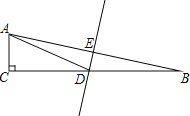
����Ŀ����ͼ����ֱ��![]() �У���֪
�У���֪![]() ��
��![]() �ߵĴ�ֱƽ���߽�
�ߵĴ�ֱƽ���߽�![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �ij���________��
�ij���________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ����С����ѧϰ��������Ǻ�������֯��һ���������ƵIJ���Dz��������߶ȵĻ�����巽�����£��ڹ���ǰ��ƽ����ѡ��һ��E��ijͬѧվ��E���ò���Dz�ù�����������Ϊ30������E���Ź���ǰ��12���F���ֲ�ù�����������Ϊ45��������������ͼ��ʾ��ͼ��ͼ���߶�AE=BF=1.6�ף���ʾ��ǵ�ѧ���۾�������ĸ߶ȣ���������ż������CD�ĸ߶ȣ���������������ο����ݣ�![]() ��.
��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
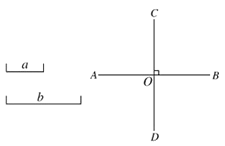
����Ŀ����ͼ����֪�߶�![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() �����ó߹棬������Ҫ����ͼ����д������������ͼ�ۼ�����
�����ó߹棬������Ҫ����ͼ����д������������ͼ�ۼ�����
��1��������![]() ��
��![]() �Ϸֱ����߶�
�Ϸֱ����߶�![]() ��
��![]() ��ʹ���Ƿֱ����߶�
��ʹ���Ƿֱ����߶�![]() ��ȣ�������
��ȣ�������![]() ��
��![]() �Ϸֱ����߶�
�Ϸֱ����߶�![]() ��
��![]() ��ʹ���Ƿֱ����߶�
��ʹ���Ƿֱ����߶�![]() ��ȣ�
��ȣ�
��2���ֱ������߶�![]() ��
��![]() ��
��![]() ��
��![]() ����õ���һ��������ͼ�Σ�
����õ���һ��������ͼ�Σ�
��3����![]() ���
���![]() ֮������������У�������̣���˵������.
֮������������У�������̣���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com