
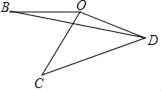
【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
【答案】 30 90 (3![]() ,﹣3)
,﹣3)
【解析】分析:(1)根据图形旋转的性质可知OB=OC=OD,再由圆周角定理即可得出结论;
(2)如图2,过点O作OM⊥CD于点M,连接EM,先根据AAS定理得出△OEB≌△OMC,故可得出OE=OM,∠BOE=∠COM,所以△OEM是等边三角形.根据OC=OD,OM⊥CD可知CM=DM.故可得出点O、C、D在以M为圆心,MC为半径的圆上.由圆周角定理可得α的大小,再根据三角函数得出结论.
详解:(1)∵线段OC,OD由OB旋转而成,
∴OB=OC=OD.
∴点B、C、D在以O为圆心,AB为半径的圆上.
∴∠BDC=![]() ∠BOC=30°.
∠BOC=30°.
(2)如图2,过点O作OM⊥CD于点M,连接EM,过点D作BF⊥BO的延长线于点F.
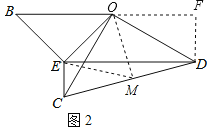
∵∠OMD=90°,
∴∠OMC=90°.
在△OEB与△OMC中,
 ,
,
∴△OEB≌△OMC.
∴OE=OM,∠BOE=∠COM.
∴∠EOM=∠EOC+∠COM=∠EOC+∠BOE=∠BOC=60°.
∴△OEM是等边三角形.
∴EM=OM=OE.
∵OC=OD,OM⊥CD,
∴CM=DM.
又∵∠DEC=90°,
∴EM=CM=DM.
∴OM=CM=DM.
∴点O、C、D、E在以M为圆心,MC为半径的圆上.
∴α=∠COD=90°,
∴∠FOD=30°,
∴OF=3![]() ,DF=3,
,DF=3,
∴点D的坐标为(3![]() ,-3).
,-3).


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
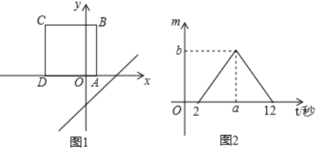
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
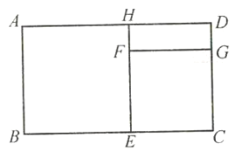
【题目】如图,长方形![]() 中,长
中,长![]() ,宽
,宽![]() ,四边形
,四边形![]() 和四边形
和四边形![]() 都是正方形.
都是正方形.
(1)求四边形![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)当![]() 、
、![]() 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某文化旅游公司为了在军运会期间更好地宣传武汉,在工厂定制了一批具有浓郁的武汉特色的商品.为了了解市场情况,该公司向市场投放![]() ,
,![]() 型商品共
型商品共![]() 件进行试销,
件进行试销,![]() 型商品成本价
型商品成本价![]() 元/件,
元/件,![]() 商品成本价
商品成本价![]() 元/件,其中
元/件,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型的件数,且不小于
型的件数,且不小于![]() 件,已知
件,已知![]() 型商品的售价为
型商品的售价为![]() 元/件,
元/件,![]() 型商品的售价为
型商品的售价为![]() 元/件,且全部售出.设投放
元/件,且全部售出.设投放![]() 型商品
型商品![]() 件,该公司销售这批商品的利润
件,该公司销售这批商品的利润![]() 元.
元.
(1)直接写出![]() 与
与![]() 之间的函数关系式:_______;
之间的函数关系式:_______;
(2)为了使这批商品的利润最大,该公司应该向市场投放多少件![]() 型商品?最大利润是多少?
型商品?最大利润是多少?
(3)该公司决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元,当该公司售完这
元,当该公司售完这![]() 件商品并捐献资金后获得的最大收益为
件商品并捐献资金后获得的最大收益为![]() 元时,求
元时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为![]() ,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
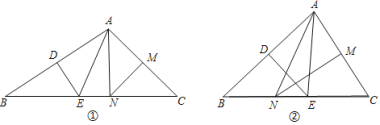
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=2n-2;④当x>-2时,nx+4n>-x+m,其中正确结论的个数是( )
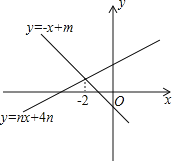
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com