练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

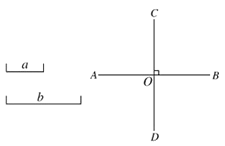
    【题目】如图，已知线段和，直线和相交于点，，利用尺规，按下列要求作图（不写作法，保留作图痕迹）：

    （1）在射线，上分别作线段，，使它们分别与线段相等，在射线，上分别作线段，，使它们分别与线段相等；

    （2）分别连接线段，，，，你得到了一个怎样的图形？

    （3）点与点之间的所有连线中，哪条最短？请说明理由.

    【答案】（1）见解析；（2）四边形EGFH是菱形；（3）GH最短，因为两点之间线段最短.

    【解析】

    （1）利用圆规分别在OC，OD上截取OE=OF=a，在OA，OB上分别截取线段OG=OH=b；
    （2）根据对角线互相垂直且平分的四边形是菱形可得四边形EGFH是菱形；
    （3）根据两点之间线段最短可得GH最短．

    解：（1）如图所示：

    （2）如图所示：

    四边形EGFH是菱形；

    （3）GH最短，因为两点之间线段最短.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】武汉某文化旅游公司为了在军运会期间更好地宣传武汉，在工厂定制了一批具有浓郁的武汉特色的商品．为了了解市场情况，该公司向市场投放，型商品共件进行试销，型商品成本价元/件，商品成本价元/件，其中型商品的件数不大于型的件数，且不小于件，已知型商品的售价为元／件，型商品的售价为元／件，且全部售出．设投放型商品件，该公司销售这批商品的利润元．

    （1）直接写出与之间的函数关系式：_______；

    （2）为了使这批商品的利润最大，该公司应该向市场投放多少件型商品？最大利润是多少？

    （3）该公司决定在试销活动中每售出一件型商品，就从一件型商品的利润中捐献慈善资金元，当该公司售完这件商品并捐献资金后获得的最大收益为元时，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＝∠2，DE⊥BC，AB⊥BC，求证：∠A＝∠3.

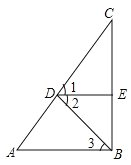
    证明：∵ DE⊥BC，AB⊥BC(已知)

    ∴∠DEC=∠ABC=90°( )

    ∴DE∥AB（_________ ___）

    ∴∠2=____ (__________ ___________)

    ∠1＝ (____________ _________)

    又∵∠1＝∠2(_____________________)

    ∴∠A＝∠3(_____________________)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形中，，，是上一点，交于点，连结．

    （1）求证：；

    （2）若，试说明四边形是菱形；

    （3）在（2）的条件下，试确定点的位置，使得，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2．则下列结论：①m＜0，n＞0；②直线y=nx+4n一定经过点（-4，0）；③m与n满足m=2n-2；④当x＞-2时，nx+4n＞-x+m，其中正确结论的个数是（　　）

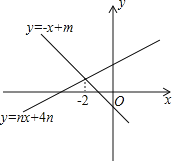
    A. 1个B. 2个C. 3个D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

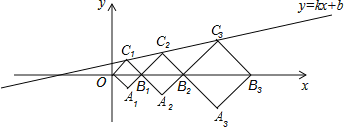
    【题目】如图，在平面直角坐标系中，正方形OA1B1C1，B1A2B2C2，B2A3B3C3，…的顶点B1，B2，B3，…在x轴上，顶点C1，C2，C3，…在直线y=kx+b上，若正方形OA1B1C1，B1A2B2C2的对角线OB1=2，B1B2=3，则点C3的纵坐标是______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

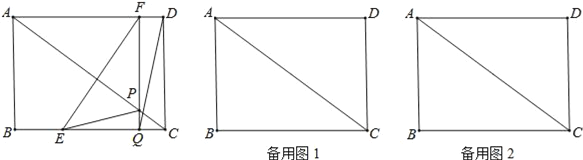
    【题目】如图，在矩形ABCD中，AB=6cm，BC=8cm．如果点E由点B出发沿BC方向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为2cm/s和1cm/s．FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t（s）（0＜t＜4）．

    （1）连结EF、DQ，若四边形EQDF为平行四边形，求t的值；

    （2）连结EP，设△EPC的面积为ycm2，求y与t的函数关系式，并求y的最大值；

    （3）若△EPQ与△ADC相似，请直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，直线y=x+1与双曲线的一个交点为P（m，6）．

    （1）求k的值；

    （2）M（2，a），N（n，b）分别是该双曲线上的两点，直接写出当a＞b时，n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：解分式不等式＜0

    解：根据实数的除法法则：同号两数相除得正数，异号两数相除得负数，因此，原不等式可转化为：

    ①或②

    解①得：无解，解②得：﹣2＜x＜1

    所以原不等式的解集是﹣2＜x＜1

    请仿照上述方法解下列分式不等式：（1）＞0；（2）＜0．

    查看答案和解析>>

    同步练习册答案