
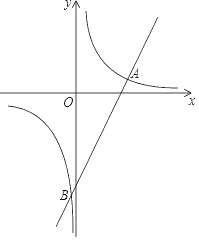
【题目】如图,一次函数y=mx+b的图象与反比例函数y=![]() 的图象交于A(3,1),B(﹣
的图象交于A(3,1),B(﹣![]() ,n)两点.
,n)两点.
(1)求该反比例函数的解析式;
(2)求n的值及该一次函数的解析式.
【答案】(1)反比例函数的解析式为y=![]() ;(2)n=﹣6,一次函数的解析式为y=2x﹣5.
;(2)n=﹣6,一次函数的解析式为y=2x﹣5.
【解析】
(1)根据反比例函数的图象经过A点,所以将A点代入反比例函数求出k的值,再将k的值代入反比例函数即可的其解析式;
(2)先将B点代入反比例函数解析式得出n=-6,再将A,B两点代入一次函数y=mx+b,即可得m,b的值,代入一次函数即可得其解析式.
解:(1)∵反比例函数y=![]() 的图象经过A(3,1),
的图象经过A(3,1),
∴k=3×1=3,
∴反比例函数的解析式为y=![]() ;
;
(2)把B(﹣![]() ,n)代入反比例函数解析式,可得
,n)代入反比例函数解析式,可得
﹣![]() n=3,
n=3,
解得n=﹣6,
∴B(﹣![]() ,﹣6),
,﹣6),
把A(3,1),B(﹣![]() ,﹣6)代入一次函数y=mx+b,可得
,﹣6)代入一次函数y=mx+b,可得
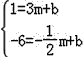 ,
,
解得![]() ,
,
∴一次函数的解析式为y=2x﹣5.


科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一般地,数轴上表示数m和数n的两点之间的距离等于![]() .如果表示数a和
.如果表示数a和![]() 的两点之间的距离是5,那么
的两点之间的距离是5,那么![]() __________;
__________;
(2)若数轴上表示数a的点位于![]() 与6之间,求
与6之间,求![]() 的值;
的值;
(3)当a取何值时,![]() 的值最小,最小值是多少?请说明理由.
的值最小,最小值是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级元旦晚会上,主持人给大家带来了一个有奖竞猜题,他在一个不透明的袋子中放了若干个形状大小完全相同的白球,想请大家想办法估计出袋中白球的个数.数学课代表小明是这样来估计的:他先往袋中放入10个形状大小与白球相同的红球,混匀后再从袋子中随机摸出20个球,发现其中有4个红球.如果设袋中有白球x个,根据小明的方法用来估计袋中白球个数的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:尺规作图:作已知角的角平分线.已知:如图,∠BAC.求作:∠BAC的角平分线AP.
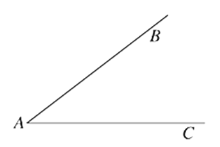
小欣的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
所以射线AP为所求
根据小欣设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP![]() DE
DE
∴ ![]() =______(________________________)(填推理的依据),
=______(________________________)(填推理的依据),
∴∠BAP=______ (________________________)(填推理的依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com