【题目】已知BD是△ABC的角平分线，ED⊥BC，∠BAC=90°，∠C=30°．
（1）求证：CE=BE；
（2）若AD=3，求△ABC的面积．
【答案】（1）见解析；（2）△ABC的面积=
．
【解析】
（1）根据直角三角形的性质和角平分线的定义证出∠C=∠DBC，然后根据等角对等边即可证出DC=DB，然后利用三线合一即可得出结论；
（2）利用30°所对的直角边是斜边的一半即可求出BD和AB，从而求出AC，然后根据三角形的面积公式计算即可．
（1）证明：∵∠A=90°，∠C=30°，
∴∠ABC=60°，
∵BD平分∠ABC，
∴∠DBC=
∠ABC=30°，
∴∠C=∠DBC，
∴DC=DB，
∵DE⊥BC，
∴EC=BE．
（2）解：在Rt△ABD中，∵∠A=90°，AD=3，∠ABD=30°，
∴BD=2AD=6，AB=
=3
，
∴DB=DC=6，
∴AC=9，
∴△ABC的面积=×
=
．
科目：初中数学 来源： 题型：
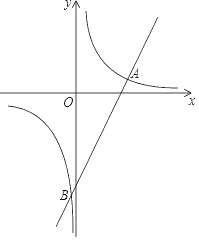
【题目】如图，一次函数y=mx+b的图象与反比例函数y=
的图象交于A（3，1），B（﹣
，n）两点．
（1）求该反比例函数的解析式；
（2）求n的值及该一次函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．
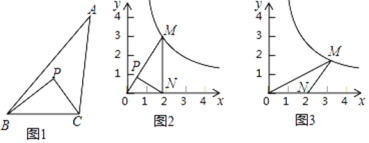
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点．
请你运用所学知识，结合上述材料，解决下列问题：
在平面直角坐标系中，点M是曲线y=
（x＞0）上的任意一点，点N是x轴正半轴上的任意一点．
（1）如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（
，3），点N的坐标是（，0）时，求点P的坐标；
（2）如图3，当点M的坐标是（3，），点N的坐标是（2，0）时，求△MON的自相似点的坐标；
（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，E、F分别是边AB、BC的中点，连接AF、DE相交于点G，连接CG．
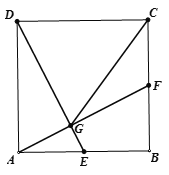
（1）求证：AF⊥DE；
（2）求证：CG=CD．
查看答案和解析>>
科目：初中数学 来源： 题型：
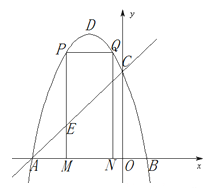
【题目】如图，抛物线
的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点.
（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N.若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ.过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）.若FG=
DQ，求点F的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数y=
x2+
x1的图象与x轴交于A、B两点，与y轴交于点C，连接AC，点P是抛物线上的一个动点，记△APC的面积为S，当S=2时，相应的点P的个数是______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，直线AB与
轴交于点A，与
轴交于点B，与直线OC：
交于点C．
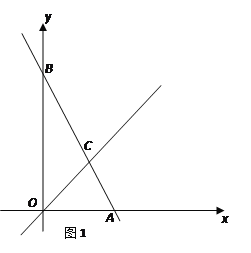
（1）若直线AB解析式为
，
①求点C的坐标；
②求△OAC的面积．
（2）如图2，作
的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．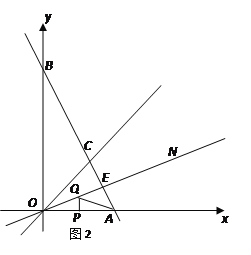
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣．某校为满足学生的阅读需求，欲购进一批学生喜欢的图书，学校组织学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类，根据调查结果绘制了统计图（未完成），请根据图中信息，解答下列问题：
（1）此次共调查了 名学生；
（2）将条形统计图补充完整；
（3）图2中“小说类”所在扇形的圆心角为 度；
（4）若该校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
